Система Orphus

.Общие понятия

Общий вид дифференциального уравнения порядка n следующий

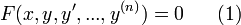
F(x, y, y',...,y^{(n)})=0~~~~~(1)

здесь

n - заданное натуральное число,

x - аргумент,

y = y(x) - неизвестная функция,

F(x,y,y1,...,yn) - заданная непрерывная функция в области Ω.

Порядком уравнения называется порядок старшей производной.

Определение. Функция 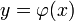y=\varphi(x), заданная на некотором промежутке X оси R называется решением (1), если :

1)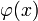\varphi(x) имеет непрерывные 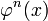\varphi^{n}(x) на X,

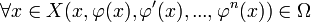2)\forall x\in X (x,\varphi(x),\varphi'(x),...,\varphi^{n}(x))\in \Omega,

3)F[x,\varphi(x),\varphi'(x),...,\varphi^{n}(x)]\equiv 0 \forall x\in X

Задача Коши, или начальная задача, для уравнения (1) ставится следующим образом: задаются начальные условия

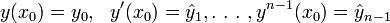
y(x_0)=y_0,~~y'(x_0)=\hat{y}_1,.~.~.~,y^{n-1}(x_0)=\hat{y}_{n-1}

и находится решение для (1) соответствующее начальным условиям.


Система Orphus

Комментарии