Общее решение линейного однородного уравнения n-ого порядка с постоянными коэффициентамив случае, когда правая часть является квазимногочленом.

Рассмотрим уравнение

где μ - заданное комплексное число, P_m(x) - заданный многочлен степени m.

Определение. Если число μ является корнем характеристического уравнения L(λ) = 0, то говорят, что в уравнении (1) имеет место резонансный случай.

Теорема. Для уравнения (1) существует и единственно решение вида

где Q_m(x) - многочлен одинаковой с P_m(x) степени m, а число k равно кратности корня μ характеристического уравнения L(λ) = 0 в резонансном случае и k = 0 в нерезонансном.

---

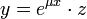Доказательство. Если , то заменой в уравнении (1) всегда можно избавиться от e^μx в правой части.

L(D)e^μxz = e^μxL(D + μ)z = e^μxP_m(x)

Отсюда L(D + μ)z = P_m(x).

Таким образом доказательство теоремы осталось провести для уравнения вида

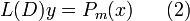
a) Нерезонансный случай: 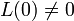. Пусть

P_m(x) = p₀x^m + ... + p_m , Q_m(x) = q₀x^m + ... + q_m .

Подставляя P_m,Q_m в уравнениие (2) и приравнивая коэффициенты при одинаковых степенях x, получаем линейную алгебраическую систему уравнений для определения неизвестных коэффициентов q₀,...,q_m

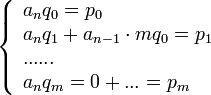
Матрица этой системы треугольная с числами 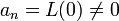по диагонали,поэтому коэффициенты Q_m(x) определяются однозначно.

б) Резонансный случай:

L(λ) = λ^k(λ^{n − k} + a₁λ^{n − k − 1} + ... + a_{n − k})

Следовательно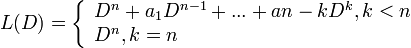

В случае k < n замена D^ky = z в уравнении (1) приводит к уравнению

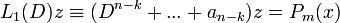
Поскольку 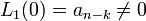, то для этого уравнения имеет место нерезонансный случа. Следовательно существует, единственное решение этого уравнения z = R_m(x).

Рассмотрим уравнение

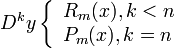
Взяв нулевые начальные условия для этого уравнения

y(0) = y'(0) = ... = y^{(k − 1)}(0) = 0

получаем единственное решение вида

.

Комментарии (показать)