Сказать "Спасибо"

Флуктуации.
Флуктуфциями называются случайные отклонения физических велечин от их средних значений.
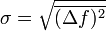 - называется среднеквадратичной флуктуацией.
- называется среднеквадратичной флуктуацией.
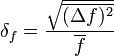 - относительная среднеквадратичная флуктуция.
- относительная среднеквадратичная флуктуция.
Во многих практически важных случаях флуктуации  физических величин имеют гауссово распределение вероятностей:
физических величин имеют гауссово распределение вероятностей:
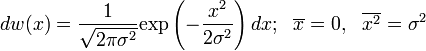 .
.Флуктуации числа частиц в выделенном объеме газа.
Среднеквадратическая флуктуация числа частиц в объеме:
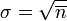
Флуктуация объема
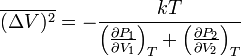
Флуктуация температуры в заданном объеме:

