Сказать "Спасибо"

Постоянство скорости света, относительность одновременности, изменение длин и промежутков времени.
Постоянство скорости света.
Скорость света в вакууме является максимально возможной скоростью в природе.
Относительность одновременности.
Рассмотрим стандартный в СТО мысленный эксперимент. Станционарный смотритель видит проходящий мимо него с релятивистской скоростю поезд, состоящий из одного вагона. Посередине вагона стоит пассажир. Пассажир держит по фонарю в каждой руке. Передняя и задняя стенка вагона - зеркала. Когда пассажир равняется со смотрителем, он мгновенно включает и выключает фонари, излучая свет в направлениях каждого из зеркал. И в ИСО пассажира и в ИСО смотрителя свет движется с одинаковой скоростью - скорость света. И в ИСО пассажира и в ИСО смотрителя испучкание обоих лучей света одновременно.
В ИСО пассажира оба луча света одновременно отражаются от зеркал и одновременно возвращаются к пассажиру.
Однако в ИСО смотрителя луч света, испущенный по направлению движения вагона, достигнет его передней стенки позже, чем луч, испущенный против направления движения вагона, достигнет его задней стенки. Однако отраженные лучи света вернутся к пассажиру одновременно.
Итак моменты отражения лучей света от стенок вагона, будучи одновременными в ИСО пассажира, не являются таковыми в ИСО смотрителя. Т.е. в СТО одновременность некоторых событий относительна.
Изменение длин и промежутков времени.
Из преобразования Лоренца имеем

или вычитая одно из другого, получаем
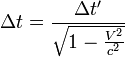
Получаем, что в движущейся системе отсчета время течет медленнее.
Как следует из преобразования Лоренца:

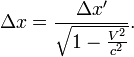
Собственной длинной стержня называется его длина в той системе отсчета, в которой он покоится. Обозначим её через 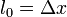 , а длину того же стержня в какой-либо системе отсчета
, а длину того же стержня в какой-либо системе отсчета 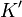 - через
- через 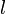 . Тогда
. Тогда
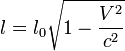 .
.Таким образом самую большую длину стержень имеет в той системе отсчета, в которой он покоится. Этот результат теории относительности называется лоренцевым сокращением.
