Сказать "Спасибо"
Предельная теорема Пуассона.
Если  и
и 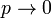 так, что
так, что 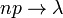 ,
, 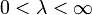 , то
, то
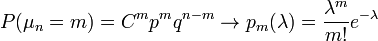
при любом постоянном 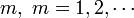 .
.
Доказательство.
Положив 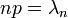 , представим вероятность
, представим вероятность 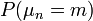 в виде
в виде

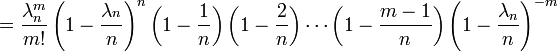 .
.Отсюда при  получим утверждение теоремы.
получим утверждение теоремы.
Если  и
и 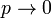 так, что
так, что 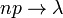 ,
, 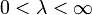 , то
, то
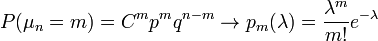
при любом постоянном 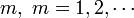 .
.
Доказательство.
Положив 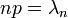 , представим вероятность
, представим вероятность 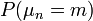 в виде
в виде

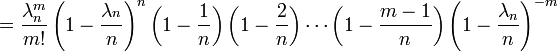 .
.Отсюда при  получим утверждение теоремы.
получим утверждение теоремы.