Сказать "Спасибо"
Сферические гармоники
Собственными функциями операторов 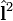 и
и 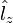 являются сферические гармоники
являются сферические гармоники 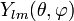 :
:
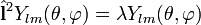 ,
,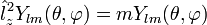 .
.Подставим в эти уравнения явные выражения для операторов в сферических координатах:
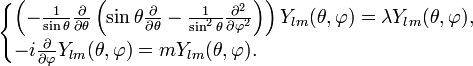
Решим эту систему дифференциальных уравнений методом разделения переменных:
Из второго уравнения получаем
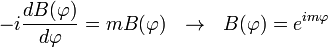
При изменении угла 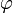 на
на 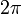 мы возвращаемся в исходную точку пространства. Поскольку волновая функция должна быть однозначной, то
мы возвращаемся в исходную точку пространства. Поскольку волновая функция должна быть однозначной, то
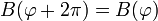
то есть
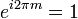 .
.Следовательно 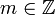 .
Подставляя
.
Подставляя
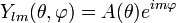
в первое уравнение системы и сокращая 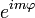 , получаем уравнение на
, получаем уравнение на  :
:
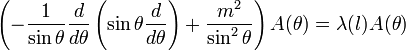 .
.Выполним замену переменной:
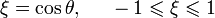 ,
,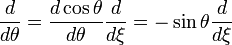 .
.Тогда
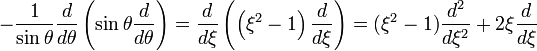 ,
,и уравнения для 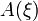 принимает вид
принимает вид
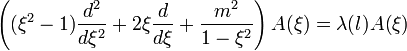 .
.Из теории уравнений математической физики следует, что расходимостей при 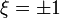 нет, только если
нет, только если
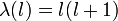 ,
,где 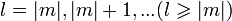 . То есть при любых
. То есть при любых 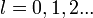 получаем уравнение
получаем уравнение
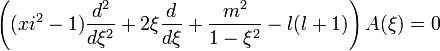
где 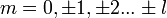 . В таком случае
. В таком случае 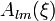 - это функция без особенностей при
- это функция без особенностей при 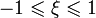 . Поскольку уравнение содержит
. Поскольку уравнение содержит  , то функции
, то функции 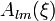 и
и 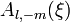 отличаются только постоянными множителем.
отличаются только постоянными множителем.
Рассмотрим два случая
a) 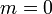 ,
,
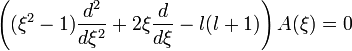 .
.Тогда решением является 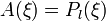 - полином Лежандра степени
- полином Лежандра степени  . Его явный вид задается формулой Родрига:
. Его явный вид задается формулой Родрига:
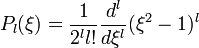
б) 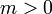 . Тогда
. Тогда 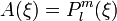 - присоединенный полином Лежандра. Для него имеем:
- присоединенный полином Лежандра. Для него имеем:
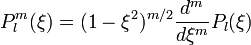 .
.Полиномы Лежандра обладают свойством ортогональности:
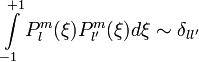 .
.Итак сферические гармоники имеют вид (для неотрицательных 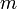 ):
):
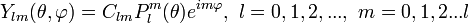 .
.Константы 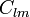 находятся из условия нормировки
находятся из условия нормировки
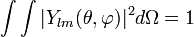 .
.Можно показать что
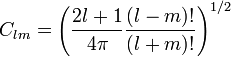 .
.Сферические гармоники с отрицательными 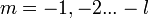 по определению принимают равными
по определению принимают равными
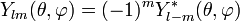
Сферические гармоники образуют полный ортонормированный базис на сфере  .
.
Барабанов 1 41