Переходы под действием периодического возмущения в дискретном и непрерывных спектрах

Рассмотрим гармоническое возмущение, оператор которого в общем случае имеет вид

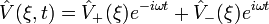$\hat{V}(\xi,t)=\hat{V}_{+}(\xi)e^{-i\omega t}+\hat{V}_{-}(\xi)e^{i\omega t}$ ,

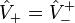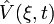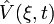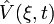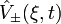где $\hat{V}_{+}=\hat{V}^{+}_{-}$ - ввиду самосопряженности оператора $\hat{V}(\xi,t)$ . Как мы увидим ниже, две части оператора $\hat{V}(\xi,t)$ описывают два различных процесса, поэтому вычисление будем проводить не для полного оператора $\hat{V}(\xi,t)$ , а для одной из его частей: $\hat{V}_{\pm}(\xi,t)=\hat{V}_{\pm}(\xi)e^{\mp i\omega t}$ . Подставляя явный вид операторов $\hat{V}_{\pm}(\xi,t)$ в

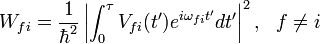
$W_{fi}=\frac{1}{\hbar^2}\left|\int_{0}^{\tau}V_{fi}(t')e^{i\omega_{fi}t'}dt'\right|^2,~~f\ne i$

и выполняя элементарное вычисление интеграла по $t$ , получим:

$W^{(\pm)}_{fi}(\tau)=\frac{4}{\hbar^2}|V_{\pm,fi}|^2\frac{\sin^2[(\omega_{fi}\mp\omega)]\tau/2}{(\omega_{fi}\mp\omega)^2}$ .

В большинстве случаев гармоническое возмущение представляет собой монохроматический световой импульс достаточно большой длительности 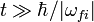$t\gg \hbar/|\omega_{fi}|$ .

Квантов 2 стр 46

Сказать "Спасибо"

Переходы под действием периодического возмущения в дискретном и непрерывных спектрах

Комментарии