В классической механике столкновения двух частиц полностью определяется их скоростями и прицельным расстоянием. В квантовой механике меняется сама постановка вопроса, так как при движении с определенными скоростями понятие траектории, а с нею и прицельное расстояние теряет смысл. Целью теории является здесь лишь вычисление вероятности того, что в результате столкновения частицы отклоняются на тот или иной угол. Мы говорим здесь о так называемых упругих столкновениях, при которых не происходит никаких превращений частиц или (если частица сложная) не меняется их внутреннее состояние.

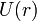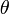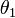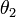Задача об упругом столкновении, как и всякая задача двух тел, сводится к задаче рассеяния одной частицы с приведенной массой в поле $U(r)$ неподвижного силового центра. Сведение осуществляется переходом к системе координат, в которой покоится центр инерции обеих частиц. Угол рассеяния в этой системе обозначим через $\theta$ . Он связан простыми формулами с углами $\theta_1$ и $\theta_2$ отклонения обеих частиц в "лабораторной" системе координат, в которой одна из частиц (вторая) до столкновения покоилась:

$\mathrm{tg}\theta_1=\frac{m_2\sin\theta}{m_1+m_2\cos\theta},~~~\theta_2=\frac{\pi-\theta}{2}$ ,

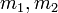где $m_1, m_2$ - массы частиц. В частности, если массы одинаковы, то получается просто

$\mathrm{tg}\theta_1=\frac{\theta}{2},~~~\theta_2=\frac{\pi-\theta}{2}$ ,

Сумма $\theta_1+\theta_2=\pi/2$ , т.е. частицы разлетаются под прямым углом. Ниже в этой главе мы пользуемся везде системой координат, связанной с центром инерции, а под $m$ подразумевается приведенная масса сталкивающихся частиц.

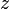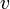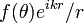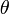Свободная частица, движущаяся в положительном направлении оси $z$ описывается плоской волной, которую мы запишем в виде $\psi=e^{ikz}$ , т.е. выберем нормировку при которой плотность потока в волне равна скорости частицы $v$ . Рассеянные частицы описываются вдали от центра расходящейся сферической волной вида $f(\theta)e^{ikr}/r$ , где $f(\theta)$ - некоторая функция угла рассеяния $\theta$ . Эту функцию называют амплитудой рассеяния. Таким образом, точная волновая функция, являющаяся решением уравнения Шредингера с потенциальной энергией 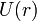$U(r)$ , должна иметь на больших расстояниях асимптотический вид

$\psi\approx e^{ikz}+\frac{f(\theta)}{r}e^{ikr}.~~~~(123.3)$

Вероятность рассеянной частицы пройти в единицу времени пройти через элемент поверхности $dS=r^{2}do$ . Её отношение к плотности в падающей волне равно

$d\sigma=|f(\theta)|^2do$ .

Это величина имеет размерность площади и называется эффективным сечением рассеяния внутри телесного угла 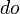$do$ . Если положить $do=2\pi\sin\theta d\theta$ , то мы получим сечение

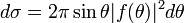
$d\sigma=2\pi\sin\theta|f(\theta)|^2 d\theta$

для рассеяния в интервале углов между 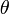$\theta$ и $\theta+d\theta$ .

Решение уравнения Шредингера, описывающее рассеяние в центральном поле 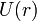$U(r)$ , должно, очевидно, быть аксиально симметричным относительно оси 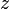$z$ - направления падающих частиц. 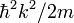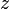Всякое такое решение может быть представлено в виде суперпозиции волновых функций непрерывного спектра, отвечающих движению в данном поле частиц с заданной энергией $\hbar^2k^2/2m$ и орбитальными моментами с различными величинами $l$ и равными нулю $z$ - проекциями (эти функции не зависят от азимутального угла вокруг оси 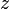$z$ , т.е. аксиально-симметричны). Таким образом, искомая волновая функция имеет форму

$\psi=\sum^{\infty}_{l=0}A_lP_l(\cos\theta)R_{kl}(r),~~~~(123.6)$

где $A_{l}$ - постоянные, а $R_{lk}(r)$ - радиальные функции, удовлетворяющие уравнению

$\frac{1}{r^2}\frac{d}{dr}\left(r^2\frac{dR_{kl}}{dr}\right)+\left[k^2-\frac{l(l+1)}{r^2}-\frac{2m}{\hbar^2}U(r)\right]R_{kl}=0$ .

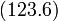Коэффициенты $A_l$ должны быть выбраны так, чтобы функция $(123.6)$ имела на больших расстояниях асимптотический вид $(123.3)$ . Покажем, что для этого надо положить

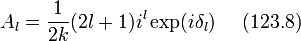
$A_l=\frac{1}{2k}(2l+1)i^{l}\exp(i\delta_l)~~~~(123.8)$

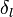где $\delta_l$ - фазовые сдвиги функции $R_{kl}$ . Тем самым будет решена задача о выражении амплитуды рассеяния через эти фазы.

Асимптотический вид функции $R_{kl}$ дается формулой

$R_{kl}\approx\frac{2}{r}\sin(kr-\frac{l\pi}{2}+\delta_{l})=$ $=\frac{1}{ir}\{(-i)^l\exp[i(kr+\delta_l)]\}$ .

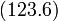Подставив это выражение, а также $(123.8)$ в $(123.6)$ , получим асимптотическое выражение волновой функции в виде

$\psi\approx\frac{1}{2irk}\sum^{\infty}_{l=0}(2l+1)P_l(\cos\theta)[(-1)^{l+1}e^{-ikr}+S_{l}e^{ikr}]$

где введено обозначение

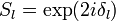$S_{l}=\exp(2i\delta_l)$ .

C другой стороны, разложение плоской волны после такого же преобразования есть

$e^{ikz}\approx\frac{1}{2ikr}\sum^{\infty}_{l=0}(2l+1)P_{l}(\cos\theta)[(-1)^{l+1}e^{-ikr}+e^{ikr}]$ .

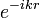Мы видим, что в разности $\psi-e^{ikz}$ все члены, содержащие множители $e^{-ikr}$ , как и следовало выпадают. Для коэффициента же при $e^{ikr}/r$ в этой разности, т.е. для амплитуды рассеяния находим

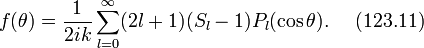
$f(\theta)=\frac{1}{2ik}\sum^{\infty}_{l=0}(2l+1)(S_l-1)P_l(\cos\theta).~~~~(123.11)$

Это формула решает задачу о выражение амплитуды рассеяния через фазы $\delta_{l}$ .

Проинтегрировав $d\sigma$ по всем углам, мы получим полное сечение рассеяния $\sigma$ , представляющая собой отношение полной величины рассеяния частицы (в единицу времени) к плотности потока в падающей волне. Подставляя $(123.11)$ в интеграл

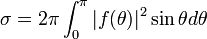
$\sigma=2\pi\int_{0}^{\pi}|f(\theta)|^2\sin\theta d\theta$

и помня, что полиномы Лежандра с различными $l$ взаимно ортогональны, а

$\int^{\pi}_0 P_l^2(\cos\theta)\sin\theta d\theta=\frac{2}{2l+1}$ ,

получим следующее выражение для полного сечения:

$\sigma=\frac{4\pi}{k^2}\sum^{\infty}_{l=0}(2l+1)\sin^2\delta_l$ .

Каждый из членов этой суммы представляет собой парциальное сечение $\sigma_l$ для рассеяния частиц с заданным орбитальным моментом $l$ . Отметим, что максимальное возможное значение этого сечения есть

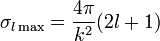$\sigma_{l\max}=\frac{4\pi}{k^2}(2l+1)$ .

Сравнив его с формулой

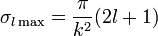$\sigma_{l\max}=\frac{\pi}{k^2}(2l+1)$ ,

видим, что число частиц, рассеянных с моментом $l$ , может оказаться в 4 раза большим числа таких частиц в падающем потоке. Это обстоятельство является чисто квантовым эффектом, связанным с интерференцией между рассеянными и нерассеянными частицами.

Ландавшиц 606

Сказать "Спасибо"

Постановка задачи рассеяния

Комментарии