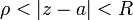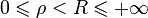Всякая функция $\omega=f(z)$ , регулярная в кольце $\rho<|z-a|<R$ , где $0\leqslant \rho < R\leqslant +\infty$ , представима в этом кольце суммой сходящегося ряда Лорана

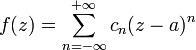$f(z)=\sum^{+\infty}_{n=-\infty}c_n(z-a)^n$ ,

коэффициенты которого определяются по формулам

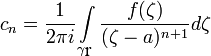$c_n=\frac{f(\zeta)}{(\zeta-a)^{n+1}}d\zeta$ , где $r\in (\rho,R),~n\in\mathbb{Z}$ ,

причем ориентация окружности $|\zeta-a|=r$ положительная.

Доказательство.

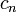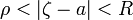Покажем что каждый коэффициент $c_n$ в формулу не зависит от выбора $r\in(\rho,R)$ . Функция $\frac{f(\zeta)}{(\zeta-a)^{n+1}}$ регулярна в кольце $\rho<|\zeta-a|<R$ . Для любых чисел $r_1,r_2:~\rho<r_1<r_2<R$ определим окружности $\gamma_{r_1},\gamma_{r_2}$ . По обобщенной теореме Коши получаем равенство

$\int\limits_{\gamma_2}\frac{f(\zeta)}{(\zeta-a)^{n+1}}=\int\limits_{\gamma_1}\frac{f(\zeta)}{(\zeta-a)^{n+1}}$

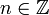что и требовалось для доказательства независимости интеграла от выбора $r\in(\rho,R)$ при каждом $n\in\mathbb{Z}$ .

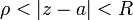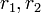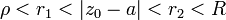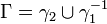Зафиксируем произвольную точку $z_0$ в кольце $\rho<|z-a|<R$ . Выберем числа $r_1,r_2$ такие, что $\rho<r_1<|z_0-a|<r_2<R$ , и окружности $\gamma_{r_1},\gamma_{r_2}$ ориентированные положительно. Тогда контур $\Gamma=\gamma_2\cup\gamma_1^{-1}$ , является границей кольца $r_1<|z-a|<r_2$ , в котором по интегральной формуле Коши получаем

$f(z_0)=\frac{1}{2\pi i}\int\limits_{\Gamma}\frac{f(\zeta)}{\zeta-z_0}d\zeta=\frac{1}{2\pi i}\int\limits_{\gamma_2}\frac{f(\zeta)}{\zeta-z_0}d\zeta-\frac{1}{2\pi i}\int\limits_{\gamma_1}\frac{f(\zeta)}{\zeta-z_0}d\zeta=I_2-I_1$ .

Рассмотрим интеграл $I_2$ . Повторяя рассуждения для вывода формулы Тейлора получаем

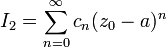
$I_2=\sum^{\infty}_{n=0}c_n(z_0-a)^n$

где

$c_n=\frac{1}{2\pi i}\int\limits_{\gamma_2}\frac{f(\zeta)}{(\zeta-a)^{n+1}}d\zeta,~~n=0,1,2,\cdots$

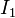Рассмотрим интеграл $I_1$ . Представим $-\frac{1}{\zeta-z_0}$ в виде ряда

$-\frac{1}{\zeta-z_0}=\frac{1}{(z_0-a)\left(1-\frac{\zeta-a}{z_0-a}\right)}=\sum^{\infty}_{n=0}\frac{(\zeta-a)^n}{(z_0-a)^{n+1}}$

По признаку Вейерштрасса ряд сходится равномерно , его можно почленно интегрировать, получаем

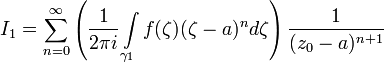
$I_1=\sum^{\infty}_{n=0}\left(\frac{1}{2\pi i}\int\limits_{\gamma_1}f(\zeta)(\zeta-a)^n d\zeta\right)\frac{1}{(z_0-a)^{n+1}}$

Заменяя в формуле номера 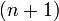$(n+1)$ на $(-m)$ получаем равенство

$I_1=\sum^{-1}_{m=-\infty}c_m(z_0-a)^m$ ,

где

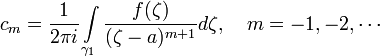
$c_m=\frac{1}{2\pi i}\int\limits_{\gamma_1}\frac{f(\zeta)}{(\zeta-a)^{m+1}}d\zeta,~~~m=-1,-2,\cdots$

Так как точка $z_0$ была выбрана в данном кольце произвольно, то складывая ряды получаем ряд Лорана.

Сказать "Спасибо"

Разложение функции, регулярной в кольце в ряд Лорана.

Комментарии