Теорема 1 (принцип максимума).

Если функция 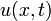$u(x,t)$ принадлежит классу $C_{x,t}^{2,1}(V_T)\cap C(\bar{V_T})$ и удовлетворяет в $V_T$ однородному уравнению теплопроводности

$u_t(x,t)-a^2\Delta_x u(x,t)=0$ ,

то для произвольной точки $(x,t)$ из $V_T$ выполняется неравенства

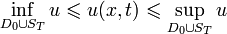$\inf_{D_0\cup S_T}u\leqslant u(x,t)\leqslant \sup_{D_0\cup S_T} u$ .

где

$D_0=\{(x,t)~:~x\in D,~t=0\}$ ,

$S_T=\{(x,t)~:~x\in\partial D,~0\leqslant t\leqslant T\}$ ,

$V_T=\{(x,t)~:~x\in D,~0<t\leqslant T\}$ .

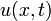Доказательство теоремы 1. Без ограничения общности можно считать, что $\sup_{\bar{V_T}}u>0$ , так как из того, что функция $u(x,t)$ удовлетворяет неравенствам, следует, что и функция $u(x,t)+\mathrm{const}$ удовлетворяет тем же неравенствам.

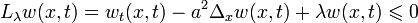Пусть $\lambda$ - произвольное положительное число. Рассмотрим функцию $w(x,t)=u(x,t)e^{-\lambda t}$ . Она удовлетворяет в $V_T$ равенству $L_\lambda w(x,t)=w_t(x,t)-a^2\Delta_x w(x,t)+\lambda w(x,t)\leqslant 0$ , и следовательно по лемме 1 выполняется неравенство

$e^{-\lambda t}u(x,t)< \sup_{(\varepsilon,\tau)\in D_0\cup S_T}e^{-\lambda\tau}u(\varepsilon,\tau),~~(x,t)\in V_T$ .

Перейдем теперь к пределу в обеих частях последнего неравенства при $\lambda\to +0$ , получаем

$u(x,t)\leqslant \sup_{(\varepsilon,\tau)\in D_0\cup S_T}u(\varepsilon,\tau),~(x,t)\in V_T$

таким образом утверждение доказано.

Лемма 1.

Пусть функция $w(x,t)$ из класса $C_{x,t}^{2,1}(V_T)\cap C(\bar{V_T})$ удовлетворяет в $V_T$ неравенству

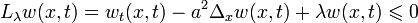$L_\lambda w(x,t)=w_t(x,t)-a^2\Delta_x w(x,t)+\lambda w(x,t)\leqslant 0$ ,

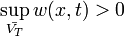при некотором $\lambda > 0$ . Тогда, если $\sup_{\bar{V_T}}w(x,t)>0$ , то для произвольной точки $(x,t)$ из $V_T$ выполняется неравенство

$w(x,t)<\sup_{D_0\cup S_T}w$

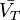Доказательство леммы 1. Прежде всего заметим, что $w(x,t)$ - непрерывная на компакте $\bar{V_T}$ функция. По этой причине значение 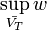$\sup_{\bar{V_T}}w$ конечно и достигается хотя бы в одной точке из 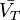$\bar{V_T}$ . Неравенство таким образом означает что значение 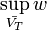$\sup_{\bar{V_T}}w$ не может достигаться в точках множества $V_T$ , то есть из равенства $w(x,t)=\sup_{\bar{V_T}}w>0$ . Тогда согласно необходимому условию максимума справедливо неравенство $\Delta_x w(x_0,t_0)\leqslant 0$ , подставляя которое в неравенство , получаем

$w_t(x_0,t_0)\leqslant -\lambda(x_0,t_0)w(x_0,t_0)<0$

Следовательно в интервале 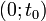$(0;t_0)$ существует момент времени $t$ , для которого $w(x_0,t)>w(x_0,t_0)$ , что противоречит выбору точки $(x_0,t_0)$ .

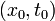Теорема 2.

Пусть функция 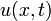$u(x,t)$ принадлежит классу $C_{x,t}^{2,1}(\mathbb{R}^n\times (0;T])$ и удовлетворяет в $[\mathbb{R}^n\times (0;T]$ однородному уровнению теплопроводности

$u_t(x,t)-a^2\Delta_x u(x,t)=0$ .

Тогда для функции справедлив принцип максимума

$\inf_{\varepsilon\in\mathbb{R}^n}u(\varepsilon,0)\leqslant u(x,t)\leqslant \sup_{\varepsilon\in\mathbb{R}^n}u(\varepsilon,0),~(x,t)\in\mathbb{R}^n\times(0;T]$ .

Доказательство теоремы 2.

Докажем только правую часть неравенства. Основная идея доказательства состоит в сведении к случаю ограниченной области при помощт барьерной функции.

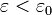Рассмотрим для произвольного фиксированного числа $\lambda>0$ вспомогательную функцию $w_{\varepsilon}(x,t)=u(x,t)e^{-\lambda t}-\varepsilon\left(|x|^2+2na^2t\right)$ , зависящую от параметра $\varepsilon>0$ . Покажем, что значение $\sup_{\varepsilon\in\mathbb{R}^n}w_\varepsilon(\varepsilon,0)$ является положительным. Из определения $C$ следует, что существует точка $x_0\in \mathbb{R}^n\setminus \{0\}$ такая, что $u(x_0,0)>\frac{3}{2}C$ . Следовательно существует число $\varepsilon_0=\frac{C}{3|x_0|^2}$ такое, что для любого $\varepsilon<\varepsilon_0$ выполняется неравенство

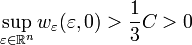
$\sup_{\varepsilon\in\mathbb{R}^n}w_\varepsilon(\varepsilon,0)>\frac{1}{3}C>0$

Отметим так же, что при $t=0$ справедливо неравенство

$w_{\varepsilon}(x,0)=u(x,0)-\varepsilon|x|^2\leqslant u(x,0)\leqslant C,~x\in\mathbb{R}^n$

Проверим выполнение в $\mathbb{R^n}\times (0;T]$ неравенства

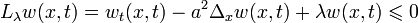
$L_{\lambda}w(x,t)=w_t(x,t)-a^2\Delta_x w(x,t)+\lambda w(x,t)\leqslant 0$

, необходимого для применения к функции 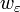$w_\varepsilon$ леммы 1:

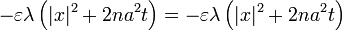
$L_\lambda w_\varepsilon(x,t)=\left(\frac{\partial}{\partial t}-a^2\Delta_x+\lambda\right)w_{\varepsilon}(x,t)=L_{\lambda}(u(x,t)e^{-\lambda t})-$ $-\varepsilon\lambda\left(|x|^2+2na^2t\right)=-\varepsilon\lambda\left(|x|^2+2na^2t\right)$

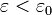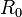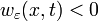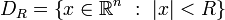Зафиксируем произвольное $\varepsilon<\varepsilon_0$ . Тогда из вида функции $w_{\varepsilon}$ и ограниченности функции $u$ следует существование числа $R_{0}$ такого, что для произвольного радиуса $R>R_0$ выполняется неравенство $w_{\varepsilon}(x,t)<0$ для $|x|=R$ и $t\in[0;T]$ . Применяя к ограниченной области $D_R=\left\{x\in\mathbb{R}^n~:~|x|<R\right\}$ и функции $w_{\varepsilon}$ лемму 1, получаем, что для точек $(x,t)\in D_R\times (0;T]$ выполняется неравенство

$w_{\varepsilon}(x,t) < \max\left\{\sup_{|\varepsilon|\leqslant R}w_{\varepsilon}(\varepsilon,0),\sup_{|\varepsilon|=R,~\tau\in[0;T]}w_{\varepsilon}(\varepsilon,\tau)\right\}\leqslant C$ .

Следовательно,

$w_{\varepsilon}(x,t)=u(x,t)e^{-\lambda t}-\varepsilon\left(|x|^2+2na^2t\right)<C,~(x,t)\in\mathbb{R}^n\times(0;T]$ ,

так как $R$ может быть сколь угодно большим. Далее совершим два предельных перехода: при $\varepsilon\to +0$ , и затем при $\lambda\to +0$ . Окончательно находим

$u(x,t) \leqslant C,~(x,t)\in\mathbb{R}^n\times(0;T]$

Сказать "Спасибо"

Принцип максимума для уравнения теплопроводности в ограниченной области.

Комментарии