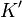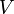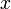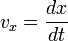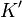Пусть система $K'$ движется относительно системы $K$ со скоростью $V$ вдоль оси $x$ . Пусть $v_x=\frac{dx}{dt}$ есть компонента скорости в системе $K$ , а $v'_x=\frac{dx'}{dt'}$ - компонента скорости той же частицы в системе $K'$ . Из преобразований Лоренца мы имеем

$dx=\frac{dx'+Vdt'}{\sqrt{1-\frac{V^2}{c^2}}}~,~~dy=dy'~,~~dt=\frac{dt'+\frac{V^2}{c}dx'}{\sqrt{1-\frac{V^2}{c^2}}}$

Разделив первые три равенства на четвертое и введя скорости

$\vec{v}=\frac{d\vec{r}}{dt}~,~~\vec{v}'=\frac{d\vec{r}'}{dt'}$

находим

$v_x=\frac{v'_x+V}{1+\frac{v'_x V}{c^2}}~,~~v_y=\frac{v'_y\sqrt{1-\frac{V^2}{c^2}}}{1+\frac{v'_x V}{c^2}}~,~~v_z=\frac{v'_z\sqrt{1-\frac{V^2}{c^2}}}{1+\frac{v'_x V}{c^2}}$

Сказать "Спасибо"

Сложение скоростей.

Комментарии