Сказать "Спасибо"
Уравнения движения частицы во внешнем электромагнитном поле как следствие принципа наименьшего действия.
Действие для заряда в электромагнитном поле имеет вид
 .
.Три пространственные компоненты 4-вектора  образуют трехмерный вектор
образуют трехмерный вектор  , называемый векторным потенциалом поля. Временную же компоненту называют скалярным потенциалом; обозначим её как
, называемый векторным потенциалом поля. Временную же компоненту называют скалярным потенциалом; обозначим её как 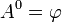 . Таким образом
. Таким образом
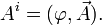
Поэтому интеграл действия можно написать в виде
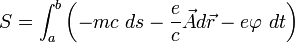
или, вводя скорость частицы 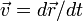 и переходя к интегрированию по времени, в виде
и переходя к интегрированию по времени, в виде
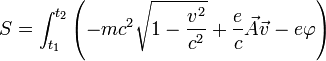 dt
dtПодынтегральное выражение есть функция Лагранжа для заряда в электромагнитном поле

Надо найти уравнения движения заряда в заданном электромагнитном поле. Эти уравнения получаются варьированием действия, т.е. даются уравнениями Лагранжа

Производная  есть обобщенный импульс частицы
Далее имеем
есть обобщенный импульс частицы
Далее имеем
 .
.Уравнение Лагранжа, следовательно имеет вид
![\frac{d}{dt}(\vec{p}+\frac{e}{c}\vec{A})=\frac{e}{c}(\vec{v}\nabla)\vec{A}+\frac{e}{c}[\vec{v}~rot~\vec{A}]-e~grad\varphi](5_teorphys/18/12.png)
Но полный дифференциал  складывается из двух частей
складывается из двух частей
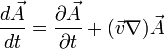
Подставляя это в предыдущее уравнение получаем
![\frac{d\vec{p}}{dt}=e(-\frac{1}{c}\frac{\partial \vec{A}}{\partial t}-grad~\varphi)+\frac{e}{c}[\vec{v}~rot~\vec{A}].](5_teorphys/18/15.png)
