Сказать "Спасибо"
Адиабатический инвариант
Для более глубокого понимания поведения частиц в слабонеоднородных внешних полях необходимо знать, что величина
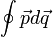
где  и
и 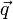 - обобщенный импульс и координата частицы, является адиабатическим инвариантом.
- обобщенный импульс и координата частицы, является адиабатическим инвариантом.
Пусть мы имеем дело с частицей, совершающей периодическое движение вроде того что происходит в постоянном магнитном поле. Пусть это движение характеризуется некоторым параметром  , определяющим свойства либо самой системы, либо же внешнего поля. Т.е. эта величина представляет собой нечто вроде ЭМ полей в предыдущих задачах. Пусть
, определяющим свойства либо самой системы, либо же внешнего поля. Т.е. эта величина представляет собой нечто вроде ЭМ полей в предыдущих задачах. Пусть  медленно (адиабатически) меняется под влиянием каких-то внешних условий,например,частица движется в слабонеоднородном поле. Т.е.
медленно (адиабатически) меняется под влиянием каких-то внешних условий,например,частица движется в слабонеоднородном поле. Т.е.
 - изменение
- изменение  за период
за период  много меньше самого
много меньше самого  . Пусть
. Пусть 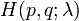 - Гамильтониан частицы.Тогда
- Гамильтониан частицы.Тогда
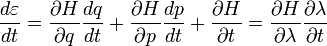
где мы воспользовались уравнениями Гамильтона  .
.
Выражение, стоящее справа зависит медленно от медленно меняющейся  и быстрых
и быстрых 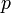 и
и  . Для выделения интересующего нас систематического хода изменения энергии следует усреднить это равенство по периоду движения. А именно свести его к уравнению:
. Для выделения интересующего нас систематического хода изменения энергии следует усреднить это равенство по периоду движения. А именно свести его к уравнению:

Вследствие медленности изменения  мы можем вынести её производную за знак усреднения.Далее
мы можем вынести её производную за знак усреднения.Далее
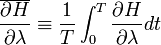
и т.к.  , то
, то  . Т.е.
. Т.е.

Припериодическом движении 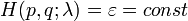 . Из этого уравнения можно найти
. Из этого уравнения можно найти 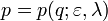 . Следовательно, дифференцируя равенство
. Следовательно, дифференцируя равенство  по
по  , получаем:
, получаем:

Откуда следует, что
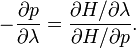
Тогда

Следовательно
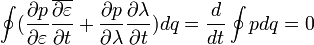
Из последнего равенства мы получаем, что следующая величина  сохраняется.
сохраняется.
