Сказать "Спасибо"
Баланс энергии системы заряженных частиц и электромагнитного поля.

-канонический тензор энергии-импульса (ТЭИ) Выполняется уравнение
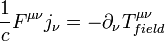
-баланс энергии частиц и ЭМ поля.
Определим 4-вектор

и подставим в него выражение для плотности 4-тока

Тогда

Воспользуемся теперь уравнением:

Умножая рассматриваемое уравнение на 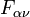 получаем, что
получаем, что

Тогда ![4\pi f^{\mu}=-\partial^{\nu}[F^{\mu\alpha}F_{\alpha\nu}+\frac{1}{4}\delta)\nu^\mu F^2]](5_teorphys/36/8.png) и уравнение баланса энергии частиц и энергии ЭМ поля верно.
и уравнение баланса энергии частиц и энергии ЭМ поля верно.
