Сказать "Спасибо"
Энергия взаимодействия двух систем зарядов, находящихся на большом расстоянии друг от друга.
Рассмотрим две системы с равными нулю суммами зарядов в каждой из них и дипольными моментами
 и
и 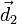 .
.
Для вычиления энергии взаимодействия, рассмотрим одну систему в поле другого

Получаем для больших расстояний

для случая, когда у одной из систем сумма зарядов не равна нулю и равна 

где  - вектор, направленный от диполя к заряду.
- вектор, направленный от диполя к заряду.
Следующий член разложения равен

где  - значение потенциала в начале координат.
- значение потенциала в начале координат.
И окончательно получаем

