Сказать "Спасибо"

Потенциалы Лиенара-Вихерта.
Определим потенциалы поля, создаваемого одним точеченым зарядом, совершающим заданное движение по траектории 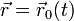
Согласно формулам запаздывающих потенциалов поле в точке наблюдения  в момент времени
в момент времени 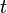 определяется состоянием движения заряда в предществующий момент
определяется состоянием движения заряда в предществующий момент 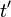 , для которого время распространения светового сигнала из точки нахождения заряда
, для которого время распространения светового сигнала из точки нахождения заряда 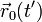 в точку наблюдения
в точку наблюдения  как раз совпадает с разностью
как раз совпадает с разностью 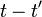 . Пусть
. Пусть  - радиус-вектор от заряда
- радиус-вектор от заряда  в точку
в точку  ; вместе с
; вместе с  он является заданной функцией времени. Тогда момент
он является заданной функцией времени. Тогда момент 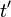 определяется уравнением
определяется уравнением
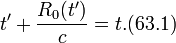
Это уравнение всегда имеет один корень
В системе отсчета, в которой в момент времени 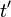 частица покоится, поле в точке наблюдения в момент
частица покоится, поле в точке наблюдения в момент 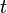 дается просто кулоновским потенциалом, т.е.
дается просто кулоновским потенциалом, т.е.
 .
.Выражения для потенциалов в произвольной системе отсчета мы получим теперь, написав такой 4-вектор, который бы при скорости  давал для
давал для  и
и  значения (63.2). Замечая, что согласно (63.1)
значения (63.2). Замечая, что согласно (63.1)  из (63.2) можно написать также и в виде
из (63.2) можно написать также и в виде
 ,
,находим, что искомый 4-вектор есть

где  - 4-скорость заряда, а 4-вектор
- 4-скорость заряда, а 4-вектор ![R^k=[c(t-t'), \vec{r}- \vec{r}']](5_teorphys/48/23.png) , причем
, причем 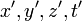 связаны друг с другом соотношением (63.1); последнее может быть записано в инвариантном виде как
связаны друг с другом соотношением (63.1); последнее может быть записано в инвариантном виде как
 .
.Переходя теперь снова к трехмерным обозначениям, получим для потенциала поля, создаваемого произвольно движущимся точечным зарядом, следующие выражения:

где 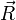 - радиус-вектор, проведенный из точки нахождения заряда в точку
- радиус-вектор, проведенный из точки нахождения заряда в точку  , и все величины в правых частях равенства должны быть взяты в момент времени
, и все величины в правых частях равенства должны быть взяты в момент времени 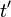 , определяющейся из (63.1). Потенциалы поля в этом виде называются потенциалами Лиенара-Вихерта.
, определяющейся из (63.1). Потенциалы поля в этом виде называются потенциалами Лиенара-Вихерта.
