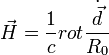Сказать "Спасибо"
Поле в квазистационнарном(ближней) и волновой (дальней) зонах.
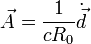
В волновой зоне
с помощью формул
![\vec{H}= \frac{1}{c}[\dot{\vec{A}}\vec{n}]~~~~\vec{E}=\frac{1}{c}[[\dot{\vec{A}}\vec{n}]\vec{n}]](5_teorphys/51/1.png)
получаем
![\vec{H}= \frac{1}{c^2R_0}[\ddot{\vec{d}}\vec{n}]](5_teorphys/51/2.png)
![\vec{E}=\frac{1}{c^2R_0}[[\ddot{\vec{d}}\vec{n}]\vec{n}]](5_teorphys/51/3.png)
В ближней зоне
Для веторного потенциала

Формулу для скалярного потенциала можно получить непосредственно с помощью общего условия
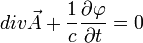
Наложенного на потенциалы. Подставляя в него (72.1) и интегрируя по времени находим

Теперь уже не представлет труда вычислить электрическое и магнитное поле