Сказать "Спасибо"
Рассеяние электромагнитных волн в дипольном приближении.
Если на систему зарядов падает электромагнитная волна, то под её влиянием заряды приходят в движение. Это движение в свою очередь сопровождается излучением во все стороны; происходит рассеяние первоначальной волны.
Рассмотрим рассеяние, производимое одним неподвижным свободным зарядом. Пусть на этот заряд падает плоская монохроматическая линейно поляризованная волна. Её электрическое поле можно записать в виде

Будем предпологать, что скорость, приобретаемая зарядом под действием поля падающей волны, мала по сравнению со скоростью света. Тогда можно считать, что сила, действующая на заряд, равна  , а силой
, а силой ![\frac{e}{c}[\vec{v}\vec{H}]](5_teorphys/56/2.png) со стороны магнитного поля можно пренебречь. Можно считать, что на него все время действует то поле, которое имеется в начале координат
со стороны магнитного поля можно пренебречь. Можно считать, что на него все время действует то поле, которое имеется в начале координат

Получаем, что
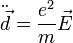
Для вычисления рассеянного излучения воспользуемся формулой  для дипольного излучения; мы имеем право сделать это, поскольку приобретаемая зарядом скорость предпологается малой. Заметим также, что частота рассеянной волны равна частоте падающей.
для дипольного излучения; мы имеем право сделать это, поскольку приобретаемая зарядом скорость предпологается малой. Заметим также, что частота рассеянной волны равна частоте падающей.
Получаем
![dI= \frac{e^4}{4\pi m^2 c^3}[\vec{E}\vec{n}']^2do](5_teorphys/56/6.png)
где  - единичный ветор в направлении рассеяния.
- единичный ветор в направлении рассеяния.
