Сказать "Спасибо"
Ортогональные преобразования - лин. преобразование,
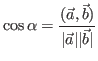 |
-
 Пусть
Пусть 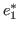 ,
,  ОНБ, покажем, что
ОНБ, покажем, что  ортогонально.
ортогонально.



-
 Ортогональное сохраняет длины и углы.
Ортогональное сохраняет длины и углы.
- Всякое ортогональное преобразование аффинное.
- Композиция ортогональных преобразований ортогональна.
- Обратный к ортогональному тоже ортогональный.
Вид ортогональных преобр. Любое ортогональное преобразование задаётся либо формулой 1, либо формулой 2:
Движение есть преобразование плоскости, сохраняющие расстояние между двумя любыми точками плоскости.

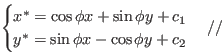
![]() . Возьмём равнобедренный прямоугольный треугольник с единичными катетами
. Возьмём равнобедренный прямоугольный треугольник с единичными катетами ![]() ,
, ![]() . Рассмотрим образ этого треугольника:
он также останется прямоугольным с единичными катетами. Своими силами определеим
. Рассмотрим образ этого треугольника:
он также останется прямоугольным с единичными катетами. Своими силами определеим
![]() :
:

![]() , поскольку одинаково преобразуют треугольник.
, поскольку одинаково преобразуют треугольник.
![]()
![]() аффинное
аффинное![]() . Где
. Где ![]() есть движение, а
есть движение, а ![]() -- сжатия к
-- сжатия к ![]() прямым.
прямым.![]() аффинное,
аффинное,
![]() и
и
![]() .
.![]() будет эллипс, гдавные оси которого
будет эллипс, гдавные оси которого ![]() и
и ![]() перпендикулярны. Утвердается, что
перпендикулярны. Утвердается, что
![]() . Действительно, малая ось есть ГМТ середин хорд, паралелльных большой оси. При аффинном преобразовании
паралелльность сохраняется, а также середина отрезка переходит в середину отрезка. Поэтому
. Действительно, малая ось есть ГМТ середин хорд, паралелльных большой оси. При аффинном преобразовании
паралелльность сохраняется, а также середина отрезка переходит в середину отрезка. Поэтому ![]() и
и ![]() перейдут в два диаметра окружности.
При этом один будет ГМТ середин хорд, паралелльных второму диаметру. Дальше используется школьная теорема о том, что диаметр, который
проходит через центр хорды, ей перпендикулярен.
перейдут в два диаметра окружности.
При этом один будет ГМТ середин хорд, паралелльных второму диаметру. Дальше используется школьная теорема о том, что диаметр, который
проходит через центр хорды, ей перпендикулярен.
![]()
![]() ,
, ![]() те самые основные направления из предыдущей леммы,
те самые основные направления из предыдущей леммы, ![]() т.е.
т.е. ![]() ,
, ![]() являются ОНБ. Положим:
являются ОНБ. Положим:
![]() ,
, ![]() и
и ![]() . Отметим на соотв. лучах точки
. Отметим на соотв. лучах точки ![]() и
и ![]() :
: ![]() . Тогда существует аффинное
. Тогда существует аффинное ![]() :
:
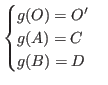
![]() ,
, ![]() определяются очевидным образом:
определяются очевидным образом:
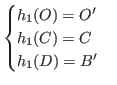

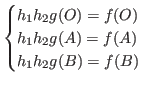
![]()

![]()
Комментарии
