Сказать "Спасибо"

3. Парабола. Параболой мы назвали линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
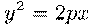 (15)
при условии
(15)
при условии

Из
уравнения (15) вытекает, что для всех точек параболы Парабола проходит через начало канонической системы координат. Эта
точка называется
вершиной параболы.
Парабола проходит через начало канонической системы координат. Эта
точка называется
вершиной параболы.
Форма
параболы известна из курса средней школы, где она встречается в
качестве графика функции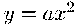 .
Отличие уравнений объясняется тем, что в канонической системе
координат по сравнению с прежней оси координат поменялись местами, а
коэффициенты связаны равенством
.
Отличие уравнений объясняется тем, что в канонической системе
координат по сравнению с прежней оси координат поменялись местами, а
коэффициенты связаны равенством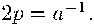
Фокусом параболы называется точка F с координатами (р/2,0) в канонической системе координат.
Директрисой параболы называется прямая с уравнением х = —р/2 в канонической системе координат (PQ на рис. 37).
Предложение 13. Расстояние от точки М(х,у), лежащей на параболе, до фокуса равно
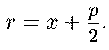 (16)
(16)
Для
доказательства вычислим квадрат расстояния от точки
М(х, у) до фокуса по
координатам этих точек

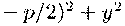 и
подставим сюда
и
подставим сюда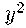 из
канонического уравнения параболы. Мы получаем
из
канонического уравнения параболы. Мы получаем

Отсюда
в силу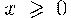 следует
равенство (16).
следует
равенство (16).
Заметим, что расстояние от точки М до директрисы по формуле (9) также равно
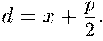
Отсюда вытекает необходимость следующего условия.
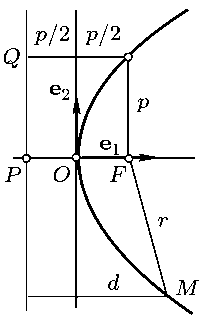
Предложение 14. Для того чтобы точка М лежала на параболе, необходимо и достаточно, чтобы она была одинаково удалена от фокуса и от директрисы этой параболы.
Докажем достаточность. Пусть точка М(х,у) одинаково удалена от фокуса и от директрисы параболы:
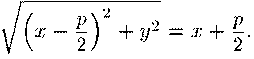
Возводя это уравнение в квадрат и приводя в нем подобные члены, мы получаем из него уравнение параболы (15). Это заканчивает доказательство.
Параболе
приписывается эксцентриситет
 В
силу этого соглашения формула
В
силу этого соглашения формула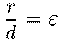 верна и для эллипса, и для гиперболы, и для параболы.
верна и для эллипса, и для гиперболы, и для параболы.
Выведем
уравнение касательной к параболе в точке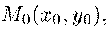 лежащей
на ней. Пусть
лежащей
на ней. Пусть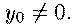 Через
точку
Через
точку проходит
график функции
проходит
график функции
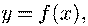 целиком
лежащий на параболе. (Это
целиком
лежащий на параболе. (Это или
же
или
же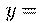
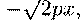 смотря
по знаку
смотря
по знаку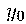 .)
Для функции
.)
Для функции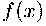 выполнено
тождество
выполнено
тождество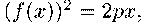 дифференцируя
которое имеем
дифференцируя
которое имеем
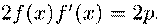
Подставляя и
и
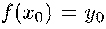 ,
находим
,
находим
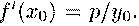 .Теперь
мы
.Теперь
мы
можем написать уравнение касательной к параболе
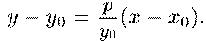
Упростим
его. Для этого раскроем скобки и вспомним, что
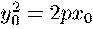 Теперь уравнение касательной принимает окончательный вид
Теперь уравнение касательной принимает окончательный вид
Y*y0 = p(x + x0). (17)
Заметим,
что для вершины параболы, которую мы исключили, положив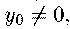 уравнение
(17) превращается в уравнение х = 0, т. е.
уравнение
(17) превращается в уравнение х = 0, т. е.
в уравнение касательной в вершине. Поэтому уравнение (17) справедливо для любой точки на параболе.
Предложение
15. Касательная к параболе в точке
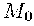 есть биссектриса угла, смежного с углом между отрезком, который
соединяет
есть биссектриса угла, смежного с углом между отрезком, который
соединяет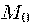 с
фокусом, и лучом., выходящим из этой точки в направлении
оси параболы
(рис. 38).
с
фокусом, и лучом., выходящим из этой точки в направлении
оси параболы
(рис. 38).

Доказательство
Рассмотрим
касательную в точке
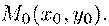 Из
уравнения (17) получаем ее направляющий вектор
Из
уравнения (17) получаем ее направляющий вектор
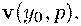 Значит,
Значит,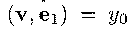 и
и
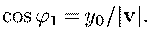 Вектор
Вектор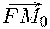 имеет компоненты
имеет компоненты
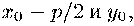 а потому
а потому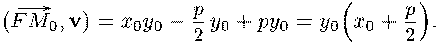
Но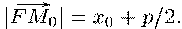 Следовательно,
Следовательно,
 Это
заканчивает
Это
заканчивает
доказательство.
Заметим,
что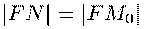 (см.
рис. 38).
(см.
рис. 38).
