Площадь криволинейного сектора.

            Пусть кривая Г задана в полярной системе координат уравнением

где  - неотрицательная и непрерывная на отрезке  функция. Тогда плоскую фигуру G, ограниченную кривой Г и, быть может, отрезками двух лучей, составляющих с полярной осью углы  и  (рис 3), назовем криволинейным сектором.

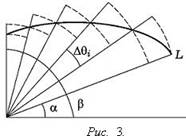
            Утверждение 2. Криволинейный сектор G – квадрируемая фигура, площадь которой S выражается формулой

Пусть  – разбиение отрезка ,  и  - соответственно наименьшее и наибольшее значения функции  на отрезке  Обозначим через  и  круговые секторы, ограниченные лучами  и дугами окружностей радиусов  и  соответственно. Если q – объединение фигур  а Q – объединение фигур  то

Так как  и  - квадрируемые фигуры, то q и Q также являются квадрируемымыми фигурами, а их площади соответственно равны

и

Отсюда следует, S(q) и S(Q) совпадают соответственно с нижней и верхней суммами Дарбу для функции  на отрезке . Поэтому:

supS(q)=infS(Q)=

Это означает, что G – квадрируемая фигура, а ее площадь S выражается формулой, приведенной в Утверждении 2.