43. Единственность представления функции степенным рядом.

Введем понятие регулярной функции. Пусть в каждой точке , где Е – множество точек комплексной плоскости, поставлено в соответствие комплексное число w. На множестве Е определена функция комплексного переменного, w=f(z).

Если >0 >0: : |z-a|<|f(z)-f(a)|<, то функцию f(z) называют непрерывной в точке а.

Функция комплексного переменного f(z) называется регулярной в точке а, если она определена в некоторой окрестности точки а и представима в некотором круге |z-a|<, >0, сходящимся к f(z) степенным рядом . (*)

Теорема. Функция f(z), регулярная в точке а, единственным образом представляется рядом (*)

Док-во: Пусть функция f(z) имеет два представления в виде степенного ряда в круге K={z: |z-a|<}, где >0, т.е.

f(z)== . (*)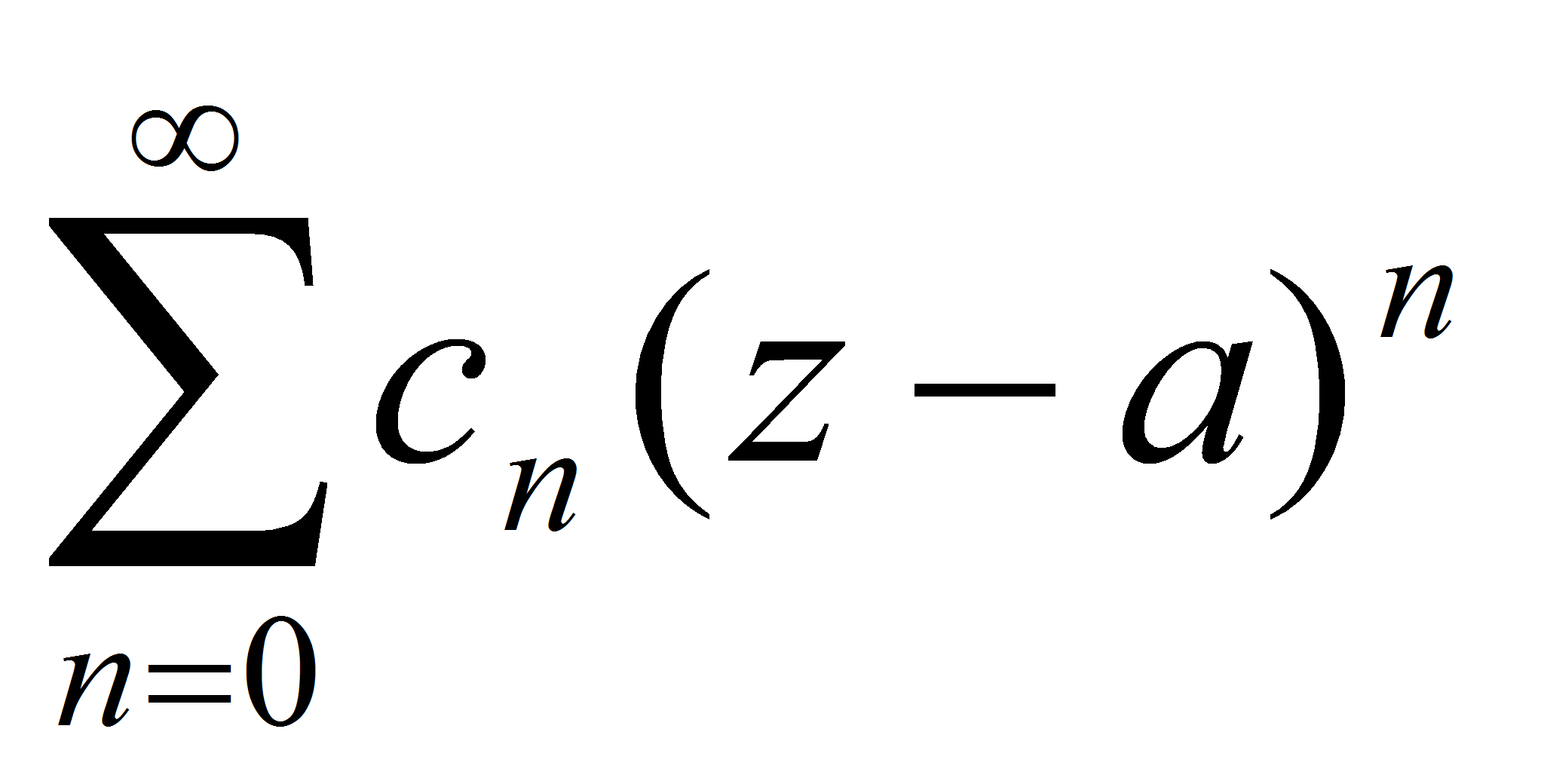

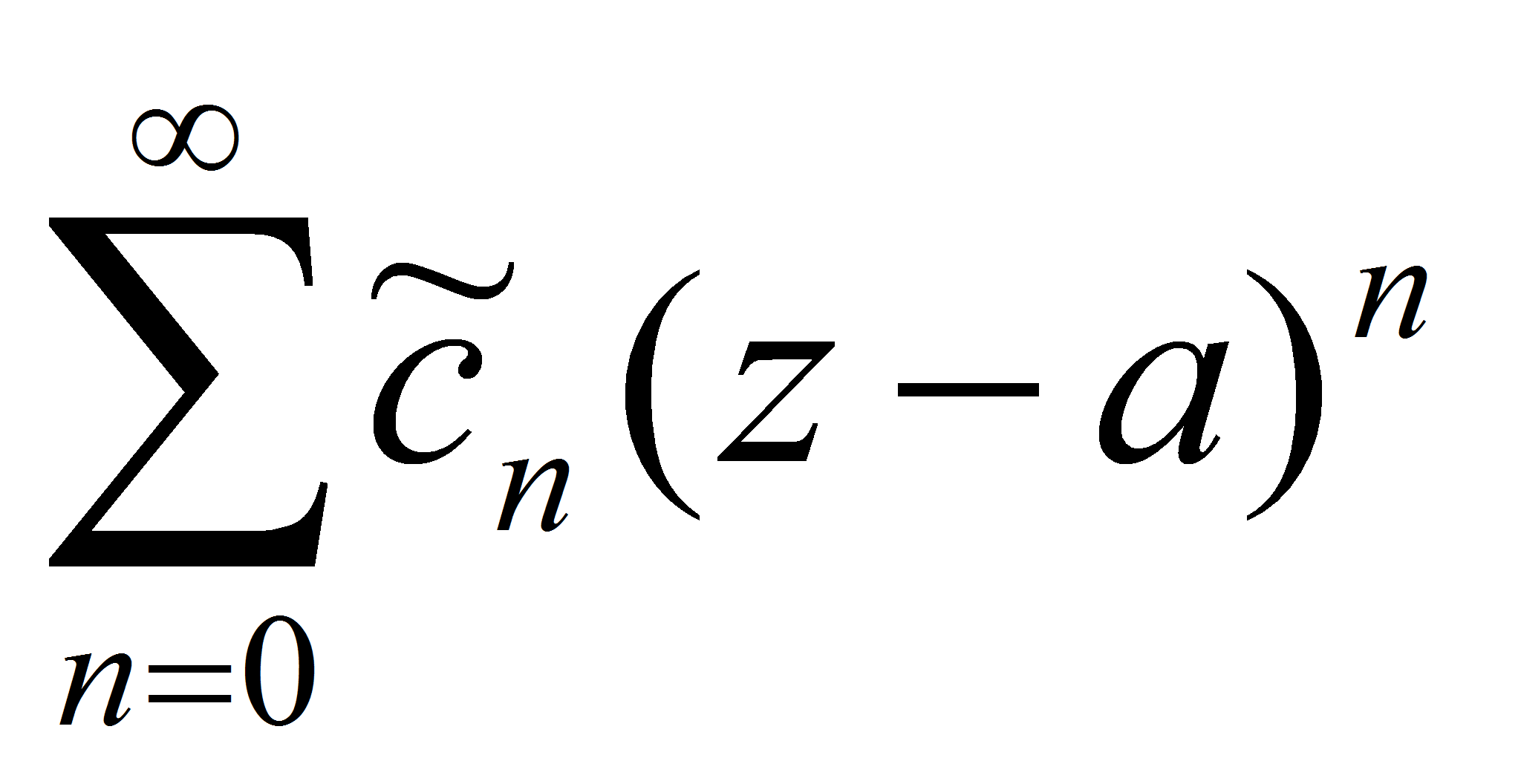Теперь докажем, что = для n=0,1,2,…

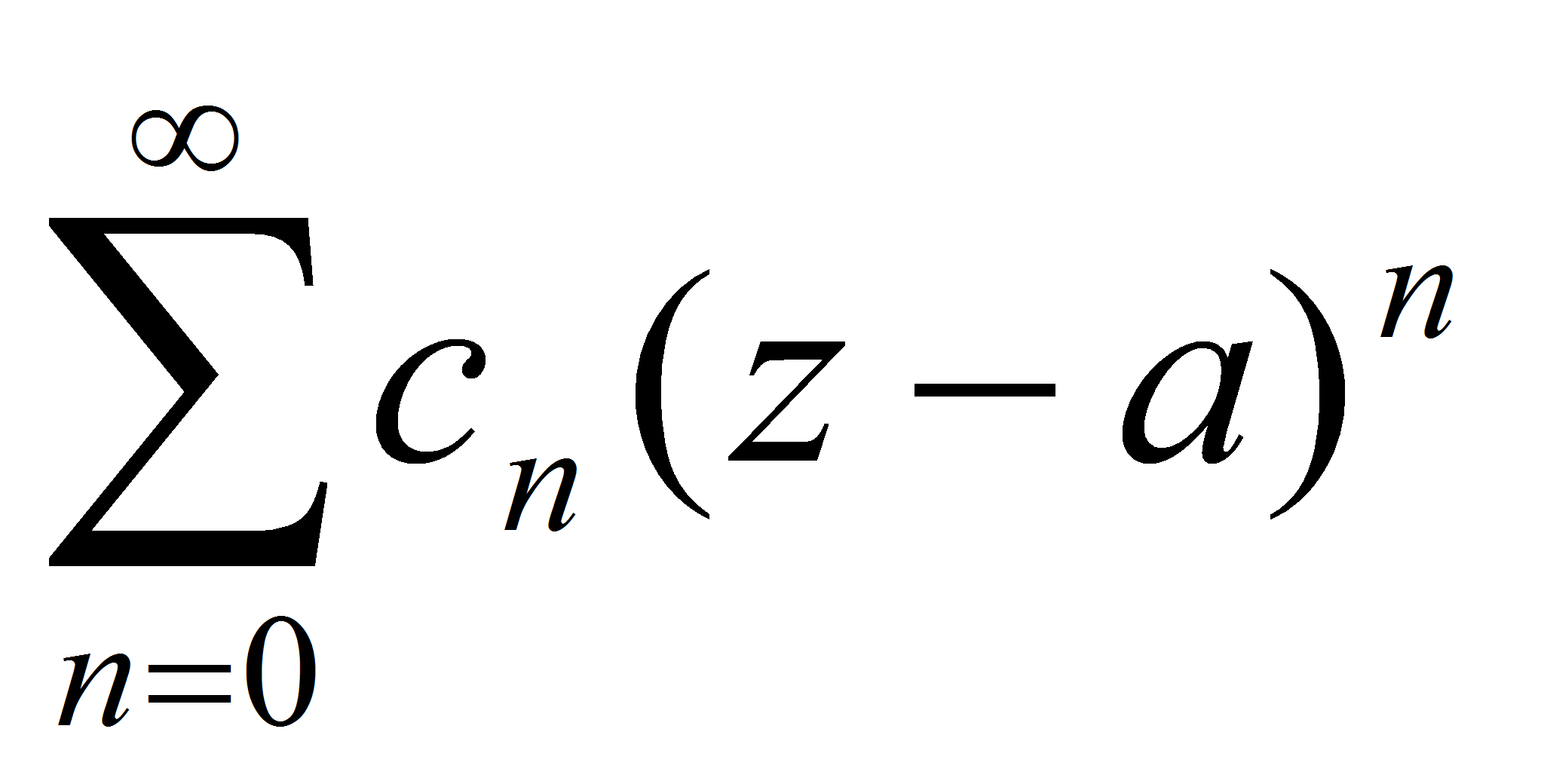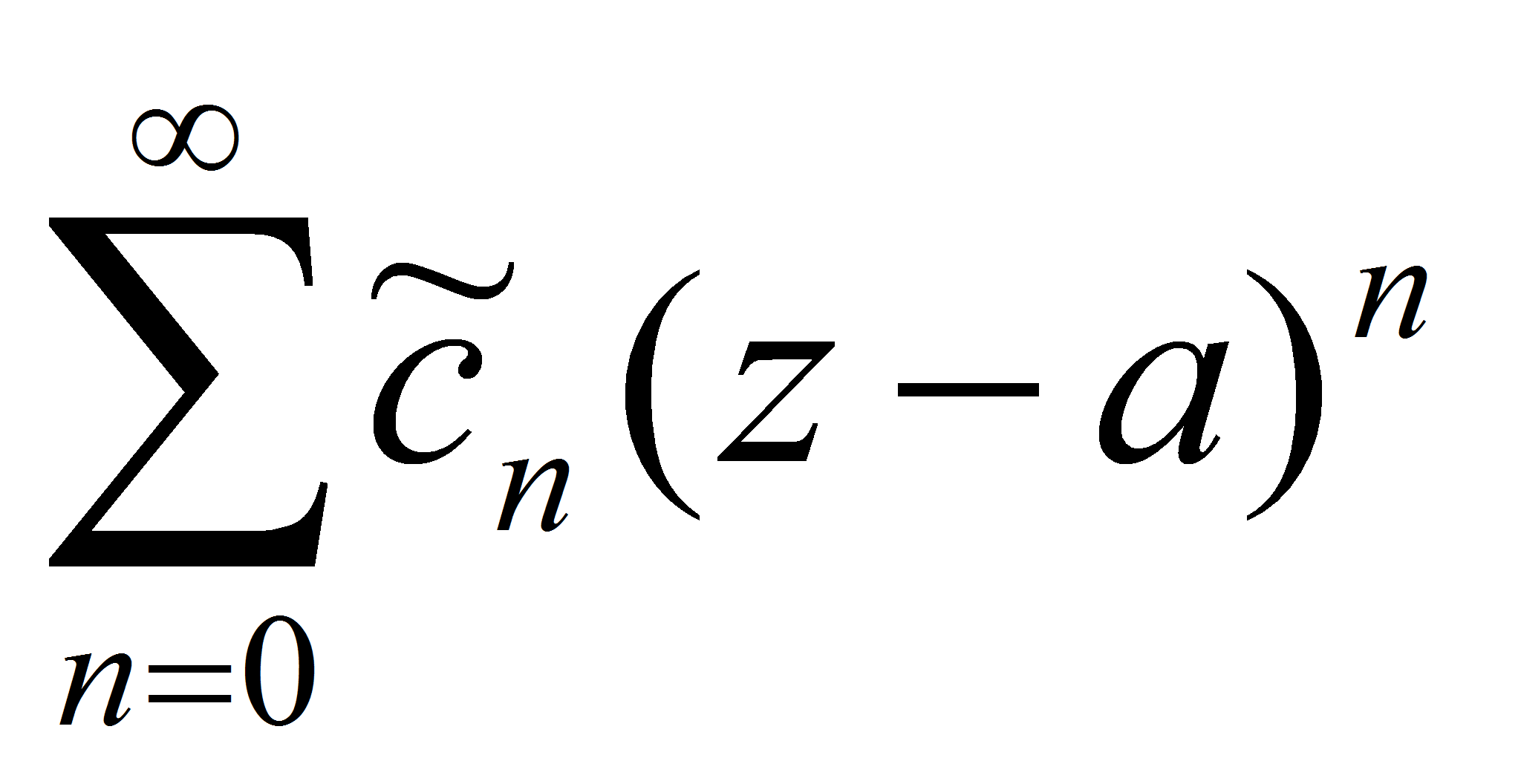По условию ряды и сходятся в круге K, и поэтому эти ряды сходятся равномерно в круге , а их общая сумма – непрерывная в круге функция. В частности, функция f(z) непрерывна в точке а. Подходя к пределу при в равенстве (*), получаем =. Отбрасывая одинаковые слагаемые и в равенстве (*), получаем после деления на z-a равенство

+(z-a)++…= +(z-a)++…,

которое справедливо в круге K с выколотой точкой a. Ряды в левой и правой части сходятся равномерно в круге .Переходя в равенстве к пределу при , получаем =. Справедливость равенства = при любом n устанавливается с помощью индукции.

Комментарии