Сказать "Спасибо"
Остаточный член в формуле Тейлора.
Пусть функция f(x)
бесконечно дифференцируема в точке ![]() . Тогда ей можно поставить в соответствие
ряд
. Тогда ей можно поставить в соответствие
ряд ![]()
![]() (1). Обозначим
(1). Обозначим
![]()
![]() (5)
(5)
![]() (6)
(6)
и назовём ![]() остаточным членом формулы Тейлора для
функции f в точке
остаточным членом формулы Тейлора для
функции f в точке ![]() . Если существует
. Если существует
![]() (7)
(7)
то согласно определению сходимости ряда ряд (1) сходится к функции f(x) в точке x, т.е.
f(x)=![]() .
(8)
.
(8)
Т е о р е м а
1. Если функции f(x), f'(x),…, ![]() непрерывны на интервале
непрерывны на интервале ![]() , где
, где ![]() , то для любого
, то для любого ![]() остаточный член формулы Тейлора для
функции f в точке
остаточный член формулы Тейлора для
функции f в точке ![]() можно представить:
можно представить:
а) в интегральной форме
![]()
![]() (t)dt (9)
(t)dt (9)
б) в форме Лагранжа
![]()
![]() ,
(10)
,
(10)
где ![]() принадлежит
интервалу с концами
принадлежит
интервалу с концами ![]() и x.
и x.
○ Формула(10)
была доказана в ![]() 18.
Докажем формулу (9) методом индукции. В силу равенств (5) и (6) нужно показать,
что
18.
Докажем формулу (9) методом индукции. В силу равенств (5) и (6) нужно показать,
что
f(x)-![]() =
=![]() +
+![]() (t)dt (11)
(t)dt (11)
Воспользуемся
равенством ![]() f'(t)dt=f(x)-
f'(t)dt=f(x)-![]() и
преобразуем его левую часть с помощью формулы интегрирования по частям:
и
преобразуем его левую часть с помощью формулы интегрирования по частям:
![]() f'(t)d(x-t) = [-f'(x)(x-t)]
f'(t)d(x-t) = [-f'(x)(x-t)]![]() =
= ![]() (x-t)f''(t)dt .
(x-t)f''(t)dt .
Таким образом,
f(x)-![]() (x-t)f''(t)dt,
(x-t)f''(t)dt,
т.е. формула (11) верна при n=1. Предположим, что формула (11) является верной для номера n-1, т.е.
f(x)- ![]()
![]()
![]() (t)dt.
(12)
(t)dt.
(12)
Преобразуем интеграл в правой части формулы (12), применив формулу интегрирования по частям:
 (t)dt=-
(t)dt=-
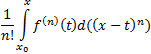 =
= ![]() +
+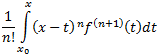 =
= ![]() +
+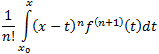
Отсюда следует, что равенство (12) можно записать в виде (11). Формула (9) доказана. ●
