Сказать "Спасибо"
Условия независимости криволинейного интеграла второго рода от пути интегрирования
Следующие три условия эквивалентны:
![]() для замкнутой ломаной
для замкнутой ломаной ![]()
![]() не зависит от ломаной
не зависит от ломаной ![]() ,соединяющей точки A
и B
,соединяющей точки A
и B
в) поле (P(x,y),Q(x,y)) потенциально, т.е. существует такая непрерывно дифференцируемая
функция U(x,y),что P(x,y) dx+Q(x,y) dy=dU
Доказательство а)=>б):

в силу условия а) интеграл не зависит от пути интегрирования
Доказательство б)=>в):
Фиксируем
точку A(x_0 ,y_0 ) а точку B(x,y)сделаем переменной, тогда ![]()
зависит
только от B
и значит в области
![]()
соединим
точку B с точкой![]() отрезком
BC
это можно сделать, т.к. G открытое
отрезком
BC
это можно сделать, т.к. G открытое
![]()
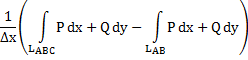
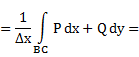
![]() применяя теорему о среднем получаем
применяя теорему о среднем получаем
![]() ,т.к.P непрерывна,то в пределе
,т.к.P непрерывна,то в пределе
![]() аналогично
для
аналогично
для ![]()
Т.к.P(x,y),Q(x,y) непрерывны в области G,то функция U непрерывно дифференциируема на G
Доказательство в)=>а):
Пусть![]() тогда
тогда
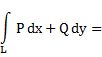
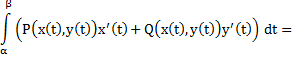
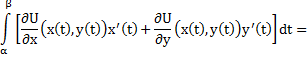
![]() т.к
начало и конец совпадают
т.к
начало и конец совпадают
Для
того чтобы дифференцируемое в области G поле было потенциальным, необходимо, а
в случае односвязной области и достаточно, чтобы ![]()
