Сказать "Спасибо"
Связь потенциальности с обращением в нуль роторного поля.
Теорема 3. Для того чтобы непрерывно дифференцируемое в области G поле а было потенциальным, необходимо, а в случае поверхностно односвязной области и достаточно, чтобы поле было безвихревым, т. е. rot a = 0.
Предварительно условимся называть
область G поверхностно односвязной если на любой простой
кусочно гладкий контур
![]() можно
натянуть кусочно гладкую поверхность
можно
натянуть кусочно гладкую поверхность![]() .
Например, пространство, из которого удалена одна точка, —
поверхностно односвязная область, но то же пространство, из которого
удалена целая прямая, не является поверхностно односвязной областью.
.
Например, пространство, из которого удалена одна точка, —
поверхностно односвязная область, но то же пространство, из которого
удалена целая прямая, не является поверхностно односвязной областью.
Необходимость. Пусть а =
 U.
Тогда
U.
Тогда
rot
a = rot
![]() U
= = 0.
U
= = 0.
Достаточность. Пусть rot a = 0 в G. Возьмем произвольную замкнутую простую ломаную
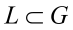 .
Так как область поверхностно односвязна, то на эту ломаную можно
натянуть кусочно гладкую поверхность
.
Так как область поверхностно односвязна, то на эту ломаную можно
натянуть кусочно гладкую поверхность
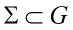 .
Применяя формулу Стокса, получаем
.
Применяя формулу Стокса, получаем
![]() (a,
dr) =
(a,
dr) =
![]() (rot
a, n)dS
= 0.
(rot
a, n)dS
= 0.
Как и в плоском
случае, индукцией по числу звеньев ломаной теперь можно доказать,
что![]() (a,
dr) = 0 по
любой ломаной L (не обязательно простой). В
силу теоремы 2 существует потенциал U(M).
(a,
dr) = 0 по
любой ломаной L (не обязательно простой). В
силу теоремы 2 существует потенциал U(M).
