Сказать "Спасибо"
Общее решение линейной однородной системы уравнений с постоянными коэффициентами в случае, когда существует базис из собственных векторов матрицы коэффициентов системы.
Рассмотрим нормальную линейную однородную систему

где  , A - квадратная комплексная матрица порядка n, x(t) - неизвестная вектор-функция с n компонентами.
, A - квадратная комплексная матрица порядка n, x(t) - неизвестная вектор-функция с n компонентами.
Лемма 1(Принцип суперпозиции). Если x(1)(t),x(2)(t) решения системы (1), а C1,C2 - произвольные комплексные числа, то вектор-функция x(t) = C1x(1)(t) + C2x(2)(t) также решение системы (1).
Лемма 2. Для того, чтобы вектор-функция x(t) = eλth была нетривиальным решением системы (1), необходимо и достаточно, чтобы λ было собcтвенным значением, а h - соответствующим ему собственным вектором преобразования A.
Теорема.
Пусть существует базис 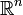 из собственных векторов h1,...,hn линейного преобразования A и пусть λ1,...,λn - соответствующие им собственные значения.
из собственных векторов h1,...,hn линейного преобразования A и пусть λ1,...,λn - соответствующие им собственные значения.
Тогда:
а) Вектор-функция x(t) вида

где C1,...,Cm произвольные комплексные постоянные, является решением системы (1).
б)Если x(t) - какое-либо решение системы (1), то найдутся такие значения постоянных C1,...,Cn, при которых x(t) задается формулой (2).
Доказательство.
а)Утверждение теоремы непосредственно следует из лемм 1 и 2.
б)Пусть x(t) - какое-либо решение (1). Так как h1,....,hn - базис в 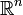 , то для
, то для 
Подставим x(t) в систему (1). Имеем
 .
.Так как h1,...,hn - линейно независимые вектора, то отсюда
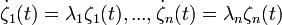
Из этих уравнений находим, что  .
.
