Система Orphus

Вариационные задачa для функционалов содержаших производные высших порядков.

Теорема. Пусть 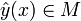\hat{y}(x)\in M является 2k раз непрерывно дифференцируемой функцией и дает слабый локальный экстремум функционала

J(y)=\int_{a}^{b}F[x, y(x), y'(x), ..., y^{(k)}(x)]dx

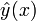Тогда \hat{y}(x) необходимо на [a,b] удовлетворяет уравнению Эйлера-Пуассона.

\sum_{i=0}^{k}(-1)^i\frac{d^i}{dx^i}\frac{\partial F}{\partial y^{(i)}}=0

Доказательство.

Необходимое условие

\delta J(y,\eta)=\int_{a}^{b}\sum_{i=0}^{k}\frac{F}{y^{(i)}}\eta^{(i)}dx=0

проинтегрировав нужное кол-во раз каждый член подынтегральной суммы приходим к утверждению теоремы.


Система Orphus

Комментарии