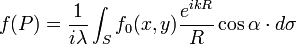Сказать "Спасибо"

Принцип Гюйгенса-Френеля.

Пусть волна света, созданная источниками, расположенными в области

z < 0

, достигла плоскости

z = 0

. Световое поле в этой плоскости нам известно. Пусть его комплексная амплитуда есть $f_0(x,y)=a_0(x,y)e^{i\varphi_0(x,y)}$ , где функции

a 0 (x, y)

и $\varphi_0(x,y)$ описывают распределение амплитуд и фаз колебаний в плоскости

z = 0

Согласно принципу Гюйгенса каждую точку $(x, y)$ плоскости $z = 0$ , куда пришла волна, можно рассматривать как источник вторичной волны. То есть можно представить себе, что волна возбуждает колебания некоторого фиктивного источника, который и переизлучает вторичную волну. Френель дополнил принцип Гюйгенса, предложив рассматривать световое колебание в любой точке наблюдения $P$ в области $z > 0$ как результат интерференции этих вторичных волн.

Поясним принцип Гюйгенса-Френеля, рассмотрев задачу - дифракции на непрозрачном экране с отверстием. Маленькая площадка

d σ

, расположенная в точке

(x, y)

на открытой части волнового фронта рассматривается как источник сферической волны: $\frac{a(x,y)}{R}e^{i(kR+\varphi(x,y))}$

где $R$ -расстояние от источника до точки наблюдения $P$ .

Согласно принятым граничным условиям, на открытой части волнового фронта, т.е. в области отверстия, волна не искажается препятствием, причем работают лишь вторичные источники, находящиеся на открытой части, не затененной непрозрачным экраном.

Амплитуда $a (x, y)$ пропорциональна также размеру переизлучающей площадки $d σ$ . Предполагается, что амплитуда колебаний в точке наблюдения пропорциональна видимой из этой точки величине площадки $d σ$ , т.е. пропорциональна $d σcosα$ . Итак, $a (x, y)˜ a 0 (x, y)cosα d σ$ , а $\varphi(x,y)=\varphi_0(x,y)$ . Таким образом, вклад элемента $d σ$ можно записать в виде

$\frac{a_0(x,y)}{R}e^{i(kR+\varphi_0(x,y))}\cos\alpha d\sigma=f_0(x,y)\frac{e^{ikR}}{R}\cos\alpha\cdot d\sigma$ .

Полное световое колебание есть результат интерференции всех вторичных волн, т.е. волн, посылаемых всеми площадками $d σ$ , расположенными в области отверстия:

$f(P)=K_0\int_{S}f_0(x,y)\frac{e^{ikR}}{R}\cos\alpha\cdot d\sigma$

Для определения константы $K 0$ рассмотрим случай, когда препятствие на пути волны отсутствует $r_0 \to \infty$ . Мы получаем

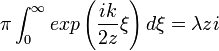
$\pi\int_{0}^{\infty}exp\left(\frac{ik}{2z}\xi\right)d\xi=\lambda zi$

Учитывая, что при отсутствии препятствия $f (P) = A 0 e i k z$ , находим $A 0 e i k z = K 0 (A 0 e i k z)λ z i$ , откуда получаем $K 0 = 1 / (i λ)$ .

Количественная формулировка принципа Гюйгенса - Френеля принимает вид

$f(P)=\frac{1}{i\lambda}\int_{S}f_0(x,y)\frac{e^{ikR}}{R}\cos\alpha\cdot d\sigma$

Сказать "Спасибо"

Принцип Гюйгенса-Френеля.

Комментарии