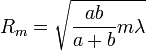Сказать "Спасибо"

Дифракция Френеля на круглом отверстии.

1. Поставим между точечным источником

S

и точкой наблюдения

P

непрозрачный экран с круглым отверстием.

Согласно Френелю, действие такого препятствия сходится к тому, что экран как-бы устраняет часть волнового фронта.

Будем предполагать, кроме того, что размеры отверстия можно менять, что дает возможность открывать любое число зон Френеля.

Если открыть первую зону Френеля, то амплитуда и интенсивность света в той же точке будут $a 1 = 2 a 0, I 1 = (2 a 0) 2 = 4 I 0$ .

При удалении от центра $P$ интенсивность будет монотонно убывать. При расширении отверстия в точку $P$ начнут проходить вторичные волны. Их интерференция с ранее пришедшими волнами вызовет уменьшение интенсивности в той же точке. Когда отверстие откроет две первые зоны Френеля, то их действия в точке $P$ практически полностью уничтожат друг-друга из-за интерференции. В точке $P$ получится темный кружок , окруженный светлым кольцом.

Вообще, при нечетном количестве открытых зон центр дифракционных колец светлый, при четном темный.

2. Определим теперь размеры и число $m$ зон Френеля, укладывающихся в отверствии $A B$ . Пусть $D$ -диаметр отверствия, а $a$ и $b$ - расстояние от его центра до точек $S$ и $P$ . Из точек $S$ и $P$ как из центров опишем сферы, проходящие через край отверстия $A B$ . Пренебрегая квадратами отрезков $O E$ и $O F$ , по известной теореме можно написать:

$(D/2)^2\approx OF\cdot 2a,~~~~~(D/2)^2\approx OE\cdot 2b$

Отсюда

$EF=EO+OF=\frac{D^2}{8}\left(\frac{1}{a}+\frac{1}{b}\right)$

Число $m$ найдется делением этого отрезка на $λ / 2$ . Оно равно

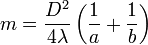
$m=\frac{D^2}{4\lambda}\left(\frac{1}{a}+\frac{1}{b}\right)$

Если $m$ целое, то $D$ будет диаметром, a $R m = D / 2$ - радиусом $m$ -ой, точнее ее внешнего края. Следовательно

$R_m=\sqrt{\frac{ab}{a+b}m\lambda}$

Сказать "Спасибо"

Дифракция Френеля на круглом отверстии.

Комментарии