Сказать "Спасибо"
Поле в фокальной плоскости линзы.
Рассмотрим точечный источник - светящуюся точку S, находящуюся в фокальной плоскости идеальной линзы, на расстоянии ξ от оптической оси.
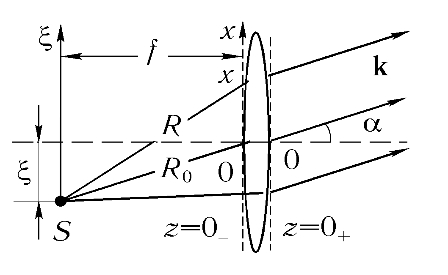
В области значений x, малых по сравнению с расстоянием R0 от источника до центра линзы O, амплитуду колебаний в сферической волне можно считать постоянной величиной
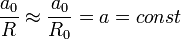 . Распределение фаз колебаний есть
. Распределение фаз колебаний есть  . Заменяя, как и ранее, сферический волновой фронт параболическим, найдем
. Заменяя, как и ранее, сферический волновой фронт параболическим, найдем

где  .
.
Играет роль, конечно, относительная фаза колебаний
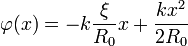
Вводя угол α и полагая его малым, так что в последнем слагаемом можно положить 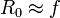 получим
получим
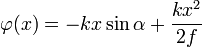
При распространении через линзу возникает дополнительный набег фазы 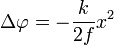 .
.
Таким образом, на выходе из линзы, т.е. в плоскости, примыкающей к линзе справа, получаем

Это формула выражает очень важный результат, волна от точечного источника, расположенного в фокальной плоскости, преобразуется линзой в волну с плоским волновым фронтом.
Рассмотрим, что из себя представляет картина поля в фокальной плоскости, если идеальная линза освещается произвольной монохроматической волной с комплексной амплитудой f(x).
Эту волну можно представить в виде суперпозиции плоских волн разных направлений αn, т.е. разных пространственных частот un = ksinαn. Каждая плоская волна, фокусируясь идеальной линзой в свою точку  , создает в этой точке колебания, амплитуда и фаза которых определяются амплитудой и фазой той плоской волны, которая в эту точку фокусируется.
, создает в этой точке колебания, амплитуда и фаза которых определяются амплитудой и фазой той плоской волны, которая в эту точку фокусируется.
Картина в фокальной плоскости линзы является преобразованием Фурье поля, падающего на линзу.
Заметим, что картина фраунгоферовой дифракции также связана преобразованием Фурье с граничным полем, причем аргументом преобразования является величина kξ / z. Таким образом, для наблюдения дифракции Фраунгофера нет необходимости удаляться от препятствия на большое расстояние - достаточно установить за препятствием линзу и наблюдать ее картину в ее фокальной плоскости, которая лишь масштабом отличается от картины дифракции Фраунгофера.
