Сказать "Спасибо"
Дифракция Фраунгофера на решетке: положение и интенсивность главных максимумов, их ширина и максимальный порядок.
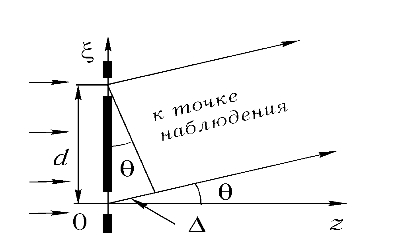
Рядом со щелью, дифракцию на которой мы рассмотрели выше,
расположим параллельно еще однну такую же щель, центр которой находится в точке ξ = d. Расстояние от второй щели до точки наблюдения меньше на величину Δ = dsinθ меньше расстояния между соответствующим элементом первой щели и точкой наблюдения. Соответственно, фаза колебаний отличается на величину α = − kΔ = − kdsinθ.
Если мы имеем решетку состоящую из N параллельно расположенных щелей (d-период решетки), суммарное колебание имеет вид
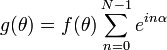
В нашем случае α = kdsinθ и мы получаем
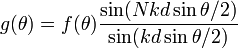
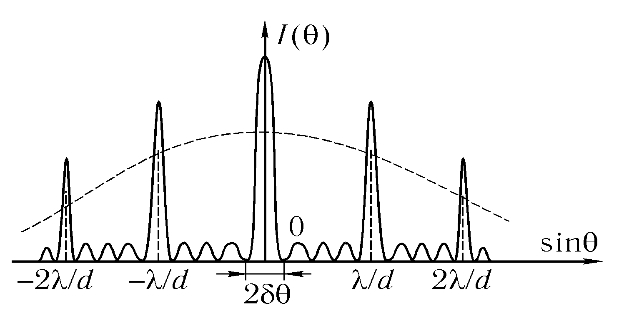
Штриховой линией показана "огибающая" - зависимость от θ первого сомножителя в I | f(θ) | 2, описывающего картину фраунгоферовой дифракции на щели ширины b.
Необходимо, чтобы разность фаз колебаний от двух соседних щелей решетки в точке наблюдения изменилась на величину δα = 2π / N.
 или
или 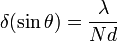
Для сравнительно небольших углов θ можно написать
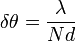
Максимальное значение порядка максимумов ограничено величиной

Реально же заметными являются лишь те дифракционные масимумы, которые лежат в пределах углов

Поэтому (при b > λ) максимальный порядок m можно оценить из условия
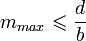
При этом общее число главных дифракционных максимумов равно приблизительно 1 + 2d / b.
