Сказать "Спасибо"
Дифракция Френеля на периодических структурах. Эффект саморепродукции.
В плоскости z = 0 + , примыкающей к структуре справа, возникает пространственно-периодическое поле f0(x)

Величина 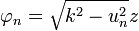 представляет собой набег фазы плоской волны, имеющей пространственную частоту un.
представляет собой набег фазы плоской волны, имеющей пространственную частоту un.
Будем полагать, что в сумме плоских волн, образующих периодическую структуру, существенно отличны от нуля, лишь значения cn, для которых  много меньше
много меньше 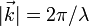 .
.
В этом случае
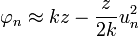
Или, поскольку  , то
, то  .
.
Существенную роль играет лишь разность фазовых набегов ( ). Мы получаем
). Мы получаем

Получаем замечательный результат: на расстояниях 
поле можно выразить следующим образом

мы наблюдаем в плоскостях zm периодическую структуру, тождественно повторяющую граничное поле f0(x).
Описанный эффект называют эффектом самовоспроизведения или эффектом Талбота.
