Сказать "Спасибо"
Принципы Фурье-оптики: представление произвольной волны в виде суперпозиции плоских волн разных направлений.
Поле плоской волны в плоскости z = 0 можно записать в виде
где множитель c = aeiux определяет как амплитуду a так и начальную фазу  волны, а через u обозначена x - компонента вектора
волны, а через u обозначена x - компонента вектора 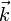 : ksinα = kx = u.
: ksinα = kx = u.
Представим граничное поле f0(x) в виде
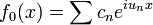
Произвольное граничное поле f0(x) представляется в виде интеграла

т.е. в виде непрерывной суммы плоских волн различных пространственных частот.
Соотношение неопределенностей должно связывать протяженность Δx граничного поля с шириной Δu его пространственного спектра:

. Пространственная протяженность граничного поля определяется характерным размером препятствия, в нашем примере - размером b отверстия в непрозрачном экране.
Поэтому ширина спектра плоских волн можно оценить так:

Разброс пространственных частот определяет разброс направлений слагаемых плоских волн за препятствием:
Откуда для малых углов

Это и есть дифракционная расходимость пучка света за отверстием размера b.
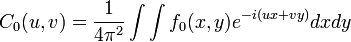
Поле на расстоянии z

в случае непрерывного спектра

