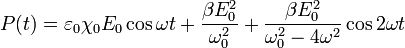Система Orphus

Генерация второй гармоники.

При малых смещениях \vec{r}, сила действующая на электрон со стороны поля ядра и стремящаяся вернуть электрон в положение равновесия, предпологалась пропорциональной смещению

\vec{f}=-k\vec{r}

Рассмотрим вначале эффекты связанные, к которым приводит появление первой нелинейной поправки

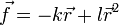
\vec{f}=-k\vec{r}+l\vec{r}^2

Уравнение движения электрона, оссцилирующего под действием поля 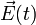\vec{E}(t) световой волны, имеет при этом вид

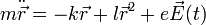
m\ddot{\vec{r}}=-k\vec{r}+l\vec{r}^2+e\vec{E}(t)

Можно перейти к скалярному уравнению

\ddot{r}+\omega_0^2r-\frac{l}{m}r^2=\frac{e}{m}E(t)

где \omega_0=\sqrt{k / m} - собственная частота малых колебаний осцилятора.

Решая этот диффур, находим что

P(t)=\varepsilon_0\chi_0E_0\cos\omega t+\frac{\beta E_0^2}{\omega_0^2}+\frac{\beta E_0^2}{\omega_0^2-4\omega^2}\cos 2\omega t

Система Orphus

Комментарии