Сказать "Спасибо"
Пространства основных и обобщенных функций.
Символом  обозначается множество бесконечно дифференцируемых финитных функций.
обозначается множество бесконечно дифференцируемых финитных функций.
Последовательность 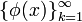 функции
функции  называется сходящейся к функции
называется сходящейся к функции 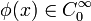 , если
, если
1)![\mathcal{9}[a,b]:supp \phi_k \subset [a,b]~~ \mathcal{8}k\in \mathbb{N}](4_matan/24/4.png)
2)![\sup_{x\in[a,b]}|\phi_k(x)^{(s)}-\phi(x)^{(s)}|\to 0](4_matan/24/5.png) при
при  .
.
Линнейненое пространство  с введенным понятием сходимости называется пространством D основных функций.
с введенным понятием сходимости называется пространством D основных функций.
Функционал f на D называется линейным, если
Функционал f на D называется непрерывным, если при 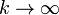 из
из
 в D следует
в D следует 
Всякий линейный непрерывный функционал на D называется обобщенной функцией.
Пространством обобщенных функций D' называется множество линейное пространство всех обобщенных функций с введенными в нем операциями сложения, умножения на число и сходимостью по следующим правилам:
1)(αf + βg,φ) = α(f,φ) + β(g,φ)
2)последовательность  ,
, 
 называется сходящиеся в D' к
называется сходящиеся в D' к 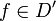 при
при 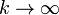 , если
, если
 в D' при
в D' при