Сечение нерезонансных реакций, закон Бете.

Для сильно взаимодействующей частицы при прохождении через границу ядра происходит резкий скачок потенциала, вызванный попаданием частицы в область действия больших сил ядерного притяжения. Можно свести к модели отражения от потенциальной ступеньки глубины $U_0$ .

Пусть нейтральная частица с энергией 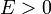$E>0$ подлетает к прямоугольной яме глубины $U_0$ . Коэффициент прохождения $D$ равен

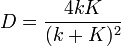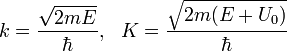
$D=\frac{4kK}{(k+K)^2}$ , где $k=\frac{\sqrt{2mE}}{\hbar},~~K=\frac{\sqrt{2m(E+U_0)}}{\hbar}$

В результате учета этих эффектов получаем

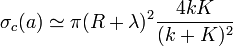
$\sigma_c(a)\simeq \pi(R+\lambda)^2\frac{4kK}{(k+K)^2}$

при малых значениях, когда 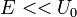$E << U_0$ , т.е. 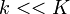$k << K$ и $\lambda=\hbar/\sqrt{2mE}>>R$ , мы имеем

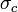$\sigma_c\simeq 4\pi\lambda^2\sqrt{E/U_0}=2\pi\hbar^2/(m\sqrt{EU_0})$

т.е. $\sigma_c$ обратно пропорционально скорости частицы - это и есть закон Бете.

Сказать "Спасибо"

Сечение нерезонансных реакций, закон Бете.

Комментарии