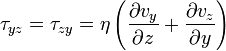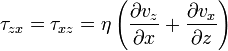Вязкое движение жидкости.

В реальных жидкостях, помимо сил нормального давления, на границах движущихся элементов жидкости действуют ещё касательные силы вязкости.

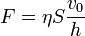
$F=\eta S\frac{v_0}{h}$

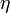$\eta$ - вязкость жидкости

$h$ - расстояние между пластинками

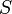$S$ - площади пластинок

$v_0$ - относительная скорость

Общая формула в случае течения в одной плоскости для касательного напряжения (сила действующая на единицу площади)

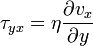
$\tau_{yx}=\eta\frac{\partial v_x}{\partial y}$

И в случае произвольного течения

$\tau_{xy}=\tau_{yx}=\eta\left(\frac{\partial v_x}{\partial y} + \frac{\partial v_y}{\partial x}\right)$ $\tau_{yz}=\tau_{zy}=\eta\left(\frac{\partial v_y}{\partial z} + \frac{\partial v_z}{\partial y}\right)$ $\tau_{zx}=\tau_{xz}=\eta\left(\frac{\partial v_z}{\partial x} + \frac{\partial v_x}{\partial z}\right)$

Сказать "Спасибо"

Вязкое движение жидкости.

Комментарии