Сказать "Спасибо"
Модуль Юнга и коэффициент Пуассона.
Модуль Юнга 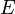 и коэффициент Пуассона
и коэффициент Пуассона  полностью характеризуют упругие свойства изотропного материала.
полностью характеризуют упругие свойства изотропного материала.
Модуль Юнга.
Сила отнесенная к единице площади, т.е 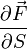 называется напряжением, действующем в соответствующей точке.
называется напряжением, действующем в соответствующей точке.
Опыт показывает, что для не слишком больших упругих деформаций напряжение  (или давление
(или давление  ) пропорционально относительному удлинению (или относительному сжатию)
) пропорционально относительному удлинению (или относительному сжатию)
 или
или 
где 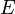 - постоянная, зависящая только от материала стержня и его физического состояния.
- постоянная, зависящая только от материала стержня и его физического состояния.
Модуль Юнга часто определяется как натяжение, которое надо приложить к стержню, чтобы его длина удвоилась.
Коэффициент Пуассона.
Опыт показывает, что под действием растягивающей или сжимающей силы  изменяются не только продольные, но и поперечные размеры стержня. Если сила
изменяются не только продольные, но и поперечные размеры стержня. Если сила  - растягивающая, то поперечные размеры стержня уменьшаются. Если она сжимающая, то они увеличиваются. Пусть
- растягивающая, то поперечные размеры стержня уменьшаются. Если она сжимающая, то они увеличиваются. Пусть  - толщина стержня до деформации,
- толщина стержня до деформации,  - после дефформации. За толщину можно принять для круглого стержня - его диаметр, для прямоугольного - одну из сторон его прямоугольного основания и т.д.
- после дефформации. За толщину можно принять для круглого стержня - его диаметр, для прямоугольного - одну из сторон его прямоугольного основания и т.д.
Если  - растягивающая, то величина
- растягивающая, то величина  называется относительным поперечным сжатием стержня.
называется относительным поперечным сжатием стержня.
Отношение относительного поперечного сжатия к соответствующему относительному продольному удлинениию назывется коэффициентом Пуассона:

Коэффициент Пуассона зависит только от материала тела и является одной из важных постоянных, характеризующих его упругие свойства.
