Сказать "Спасибо"
Его интерпретация на основе молекулярно кинетической теории.
Рассмотрим столкновения молекул идеального газа с неподвижной стенкой. Выделим группу молекул имеющую скорость  . В единице объема газа число таких молекул равна
. В единице объема газа число таких молекул равна  . Для одной молекулы
. Для одной молекулы 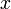 - компонента импульса равна
- компонента импульса равна  .
В результате упругого столкновения со стенкой молекула передает импульс
.
В результате упругого столкновения со стенкой молекула передает импульс 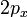 . За время
. За время  до стенки долетят молекулы, удаленные от неё на
до стенки долетят молекулы, удаленные от неё на 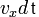 . Их число есть
. Их число есть  , а передают они стенке импульс
, а передают они стенке импульс  . Суммируя по всем группам молекул, получим полный импульс, передаваемый стенке за время
. Суммируя по всем группам молекул, получим полный импульс, передаваемый стенке за время  :
:
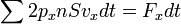 .
.Отсюда следует, что давление равно

В итоге
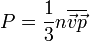
Для молекулы массы 
 Можно ввести связь между средней энергией и температурой
Можно ввести связь между средней энергией и температурой
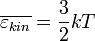
где 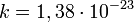 Дж/К.
Дж/К.
