Зависимость теплоемкости газов от температуры.

В частности, для газа, состоящего из двухатомных молекул, теплоемкость складывается из поступательной, вращательной и колебательной частей и равна

$C_V=\underbrace{\frac{3}{2}R}_{post.}+\underbrace{\frac{2}{2}R}_{vrach.}+\underbrace{\left(\frac{1}{2}R+\frac{1}{2}R\right)}_{kol.}=\frac{7}{2}R$ .

Это значит, что теплоемкость должна быть постоянной. Вместе с тем опыт говорит, что теплоемкость зависит от температуры.

При понижении температуры "замораживаются" сначала колебательные степени свободы, а затем и вращательные степени свободы.

Согласно законам квантовой механики энергия гармонического осциллятора с классической частотой $\omega$ может принимать только дискретный набор значений

$\varepsilon_n=\left(n+\frac{1}{2}\right)\hbar\omega$

В соответствии с распределением Гиббса вероятность того, что молекула обладает энергией 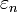$\varepsilon_n$ , равна

$W_n=\frac{1}{Z}\exp\left(-\frac{\varepsilon_n}{kT}\right)$

Найдем статистическую сумму

$Z=\frac{\exp(-\hbar\omega/2kT)}{1-\exp(-\hbar\omega/kT)}$

Зная величину $Z$ можно найти среднюю энергию молекулы:

$\overline{\varepsilon}=\frac{1}{2}\hbar\omega \mbox{cth}\left(\frac{\hbar\omega}{2kT}\right)$

Для молярной теплоемкости получаем

$C_V=\left(\frac{\partial E}{\partial T}\right)_V=R\left(\frac{\hbar\omega}{2kT}\right)^2\frac{1}{\mbox{sh}^2(\hbar\omega/2kT)}$

получаем, что теплоемкость убывает до нуля. Причина - это дискретность уровней гармонического осциллятора.

Сказать "Спасибо"

Зависимость теплоемкости газов от температуры.

Комментарии