Сказать "Спасибо"
Вывод формулы Пуассона с помощью преобразования Фурье.
Преобразованием Фурье непрерывной и абсолютно интегрируемой в  , функции
, функции  называется функция
называется функция
 ,
,где  .
.
Если функция 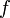 имеет непрерывную производную
имеет непрерывную производную 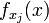 , также абсолютно интегрируемую в
, также абсолютно интегрируемую в  , то преобразование Фурье функции
, то преобразование Фурье функции 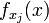 связано с преобразованием Фурье функции
связано с преобразованием Фурье функции  следующим образом:
следующим образом:
 .
.Аналогично, при соответствующих предположениях, преобразование Фурье функции 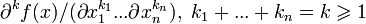 , имеет вид
, имеет вид
 .
.Поэтому в частности, преобразование Фурье от оператора Лапласа от функции 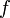 .
.
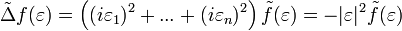 .
.
Обратное преобразование Фурье:
 .
.Перейдем к рассмотрению задачи рассмотрим однородное уравнение
 ,
,

пусть решение  задачи существует. Цель получить явное выражение функции
задачи существует. Цель получить явное выражение функции  через
через  .
Умножая тождество (2.1) при
.
Умножая тождество (2.1) при 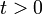 на
на  , где
, где  - произвольная точка из
- произвольная точка из  , и интегрируя полученное равенство по
, и интегрируя полученное равенство по 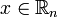 , получим
, получим
 ,
,где  - зависящее от параметра
- зависящее от параметра 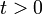 преобразование Фурье функции
преобразование Фурье функции  по переменным
по переменным 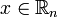 :
:
 .
.Аналогично из (2.2) имеем равенство
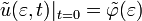 .
.
Получаем для функции  при произвольном фиксированном
при произвольном фиксированном 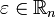 есть задача для обыкновенного дифференциального уравнения. Ее решение имеет вид
есть задача для обыкновенного дифференциального уравнения. Ее решение имеет вид
 .
.Следовательно решением изначальной задачи с помощью обратного преобразования Фурье представляется в виде
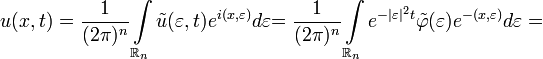
![\int\limits_{\mathbb{R}_n}\varphi(y)\left[\frac{1}{(2\pi)^n}\int\limits_{\mathbb{R}_n}e^{-|\varepsilon|^2t} e^{i(x-y,\varepsilon)}d\varepsilon\right]dy=\int\limits_{\mathbb{R}_n}K(x-y,t)\varphi(y)dy](6_urmat/31/36.png) ,
,где
 .
.Для функции 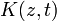 имеем равенство
имеем равенство
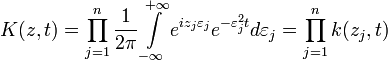
где

Так как
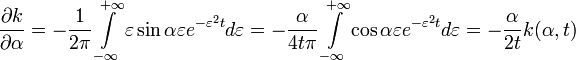 ,
,то 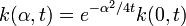 . Но
. Но
 ,
,поэтому
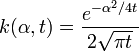
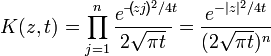
и следовательно