Сказать "Спасибо"
Единственность классического решения первой начально-краевой задачи для уравнения теплопроводности в ограниченной области.
Теорема 1.
Пусть  - ограниченная область в
- ограниченная область в 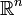 . Если решение
. Если решение 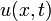 смешанной задачи для уравнения теплопроводности
смешанной задачи для уравнения теплопроводности

с начальными условиями

с граничными условиями первого рода
![u(x,t)|_{x\in\partial D}=v(x,t),~v(x,t)\in C(\partial D\times [0;T])](6_urmat/34/5.png)
существует в классе функций 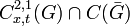 , то оно единственно в этом классе и непрерывно зависит от начальных и граничных данных (в равномерной метрике).
, то оно единственно в этом классе и непрерывно зависит от начальных и граничных данных (в равномерной метрике).
Доказательство теоремы 1.
Единственность. Пусть 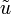 и
и 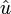 - решение задачи. Тогда их разность
- решение задачи. Тогда их разность 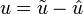 удовлетворяет однородному уравнению теплопроводности с однородными начальными и граничными условиями:
удовлетворяет однородному уравнению теплопроводности с однородными начальными и граничными условиями:
 ,
, ,
, .
.Согласно принципу максимума в ограниченной области выполняются неравенства
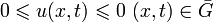
Следовательно  в
в  .
.
Непрерывная зависимость. Пусть теперь 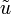 и
и 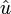 - решение задачи Коши отвечающие различным начально-краевым данным:
- решение задачи Коши отвечающие различным начально-краевым данным:  и
и  соответственно. Тогда разность
соответственно. Тогда разность 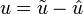 является решением смешанной задачи для однородного уравнения теплопроводности
является решением смешанной задачи для однородного уравнения теплопроводности

с начальными условиями
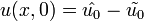
и граничными условиями
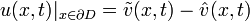 .
.Воспользуемся для функции 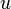 принципом максимума, получаем оценку
принципом максимума, получаем оценку
![|\tilde{u}(x,t)-\hat{u}(x,t)|\leqslant \max\left\{\sup_{\bar{D}}|\tilde{u_0}-\hat{u_0},\sup_{\partial D\times [0;T]}|\tilde{v}-\hat{v}|\right\},~~(x,t)\in\bar{G}](6_urmat/34/25.png) ,
,что означает непрерывную зависимость решения от начальных и краевых данных в равномерной метрике. Из принципа единственности максимума в неограниченной области вытекает следующее
Теорема 2.
Если решение задачи Коши
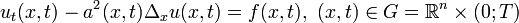 ,
,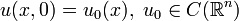
с ограниченными начальными данными 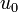 существует в классе функций
существует в классе функций  , то оно единственно в нем и непрерывно зависит от начальных данных.
, то оно единственно в нем и непрерывно зависит от начальных данных.
