Классификация и приведение к каноническому виду уравнений второго порядка с вещественными переменными коэффициентами в случае двух независимых переменных.
Уравнение называется линейным относительно старших производных, если оно имеет вид

где 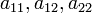 являются функциями
являются функциями  и
и  .
.
Если коэффициенты 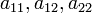 не только зависят от
не только зависят от  и
и  а являются подобно
а являются подобно  , функциями
, функциями  , то такое уравнение называется квазилинейным.
, то такое уравнение называется квазилинейным.
Уравнение называется линейным, если оно линейно как относительно старших производных  , так и относительно функции
, так и относительно функции 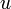 и её первых производных
и её первых производных  :
:
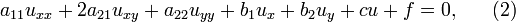
где  - функции только
- функции только 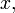 и
и  . Если коэффициенты уравнения (2) не зависят от
. Если коэффициенты уравнения (2) не зависят от  и
и  , то оно представляет собой линейное уравнение с постоянными коэффициентами. Уравнение называется однородным, если
, то оно представляет собой линейное уравнение с постоянными коэффициентами. Уравнение называется однородным, если  .
.
C помощью преобразования переменных

допускающего обратное преобразование, мы получаем новое уравнение, эквивалентное исходному. Рассмотрим уравнение, линейное относительно старших производных вида (1) с двумя независимыми переменными  и
и  :
:

Преобразуя производные к новым переменным, получаем
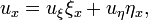
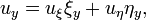
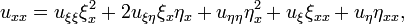
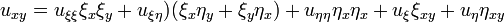 ,
,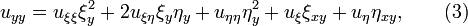
Подставляя значения производных из (3) в уравнение (1), будем иметь

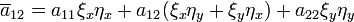 ,
,
a функция  не зависит от вторых производных. Заметим, что если исходное уравнение линейно, т.е.
не зависит от вторых производных. Заметим, что если исходное уравнение линейно, т.е.
 ,
,то  имеет вид
имеет вид

т.е. уравнение остается линейным.
Выберем переменные  и
и  так, чтобы коэффициент
так, чтобы коэффициент  был равен нулю. Рассмотрим уравнение с частными производными 1-го порядка
был равен нулю. Рассмотрим уравнение с частными производными 1-го порядка

Пусть  - какое-нибудь частичное решение этого уравнения. Если положить
- какое-нибудь частичное решение этого уравнения. Если положить  , то коэффициент
, то коэффициент  , очевидно, будет равен нулю. Таким образом, упомянутая выше задача о выборе новых независимых переменных связана с решением уравнения (5).
, очевидно, будет равен нулю. Таким образом, упомянутая выше задача о выборе новых независимых переменных связана с решением уравнения (5).
Докажем следующие леммы.
1. Если  - какое-нибудь частное решение этого уравнения
- какое-нибудь частное решение этого уравнения
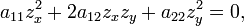
то соотношение  представляет собой общий интеграл обыкновенного дифференциального уравнения
представляет собой общий интеграл обыкновенного дифференциального уравнения
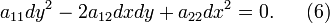
2. Если  представляет собой общий интеграл обыкновенного дифференциального уравнения
представляет собой общий интеграл обыкновенного дифференциального уравнения
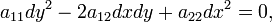
то функция  удовлетворяет уровнению (5).
удовлетворяет уровнению (5).
Докажем первую лемму. Посколько функция  удовлетворяет уровнению (5), то равенство
удовлетворяет уровнению (5), то равенство

является тождеством: оно удовлетворяется для всех 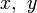 в той области, где задано решение. Соотношение
в той области, где задано решение. Соотношение  является общим интегралом уравнения (6), если функция
является общим интегралом уравнения (6), если функция  , определенная из неявного соотношения
, определенная из неявного соотношения  , удовлетворяет уравнению (6). Пусть
, удовлетворяет уравнению (6). Пусть

есть эта функция; тогда
![\frac{dy}{dx}=-\left[\frac{\varphi_x(x, y)}{\varphi_y(x, y)}\right]_{y=f(x,C)},~~~~~(8)](6_urmat/4/56.png)
где квадратные скобки и индекс  указывают, что в правой части равенства (8) переменная
указывают, что в правой части равенства (8) переменная  не является независимой переменной, а имеет значение, равное
не является независимой переменной, а имеет значение, равное  . Отсюда следует, что
. Отсюда следует, что  удовлетворяет уравнению (6), так как
удовлетворяет уравнению (6), так как
![a_{11}\left(\frac{dy}{dx}\right)^2-2a_{12}\frac{dy}{dx}+a_{22}=\left[a_{11}\left(-\frac{\varphi_x}{\varphi_y}\right)^2-2a_{12}\left(-\frac{\varphi_x}{\varphi_y}\right)+a_{22}\right]_{y=f(x,C)}=0](6_urmat/4/61.png) ,
,поскольку выражение в квадратных скобках равно нулю при всех значениях  а не только при
а не только при  .
.
Докажем вторую лемму. Пусть  - общий интеграл уравнения (6). Докажем, что
- общий интеграл уравнения (6). Докажем, что

для любой точки 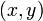 . Пусть
. Пусть 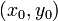 - какая-нибудь заданная точка. Если мы докажем, что в ней удовлетворяется равенство
- какая-нибудь заданная точка. Если мы докажем, что в ней удовлетворяется равенство 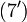 , то отсюда в силу произвольности
, то отсюда в силу произвольности 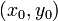 будет следовать равенство (7') есть тождество и функция
будет следовать равенство (7') есть тождество и функция  является решением уравнения (7'). Проведем через точку
является решением уравнения (7'). Проведем через точку 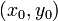 интегральную кривую уравнения (6), полагая
интегральную кривую уравнения (6), полагая  и рассматривая кривую
и рассматривая кривую  . Очевидно, что
. Очевидно, что  . Для всех точек кривой имеем
. Для всех точек кривой имеем
![a_{11}\left(\frac{dy}{dx}\right)^2-2a_{12}\frac{dy}{dx}+a_{22}=\left[a_{11}\left(-\frac{\varphi_x}{\varphi_y}\right)^2-2a_{12}\left(-\frac{\varphi_x}{\varphi_y}\right)+a_{22}\right]_{y=f(x, C_0)}=0.](6_urmat/4/75.png)
Полагая в последнем равенстве 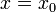 , получаем
, получаем

что и требовалось доказать.
Уравнение (6) называется характеристическим для уравнения (1), а его интегралы - характеристиками.
Полагая  , где
, где 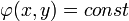 есть общий интеграл уравнения (6), мы обращаем в нуль коэффициент при
есть общий интеграл уравнения (6), мы обращаем в нуль коэффициент при  . Если
. Если  является другим общим интегралом уравнения (6), независимым от
является другим общим интегралом уравнения (6), независимым от  , то полагая
, то полагая  , мы обратим в нуль также и коэффициент при
, мы обратим в нуль также и коэффициент при  .
.
Уравнение (6) распадается на два уравнения


Знак подкоренного уравнения определяет тип уравнения (1)
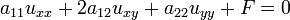
Это уравнение мы будем называть в точке  уравнением
уравнением
гиперболического типа, если в точке 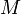
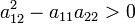 ,
,
параболического типа, если в точке 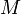
 ,
,
эллиптического типа, если в точке 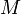
 .
.