Сказать "Спасибо"
Цифровые подписи, требования к ним и характеристики на примере стандарта ГОСТ Р 34.10-2001
Российский стандарт ЭЦП основан на криптосистеме типа Эль-Гамаль.
В качестве группы используется группа точек на эллиптической кривой над конечным полем(группа должна быть порядка  элементов).
элементов).
Пусть имеются две стороны  и
и 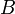 и между ними канал связи. Пусть сторона
и между ними канал связи. Пусть сторона  желает передать сообщение
желает передать сообщение  стороне
стороне 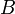 и подписать его. Сторона
и подписать его. Сторона 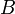 должна проверить правильность подписки, то есть аутентифицировать сторону
должна проверить правильность подписки, то есть аутентифицировать сторону  .
.
Формирование пары открытого и закрытого ключей
- Выбрать простое число
 ,
,
- Записать уравнение эллиптической кривой
-
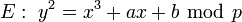 ,
,
которое определяет группу точек эллиптической кривой  .
.
Для того, чтобы выбрать группу, Alice задает два случайныx числа  , либо эллиптический инвариант
, либо эллиптический инвариант 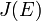 в интервале
в интервале  :
:
-
 ,
,
и для нахождения  вычисляется
вычисляется
-
 .
.
- подобрать числа натуральное
 и простое
и простое 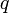 такие, что
такие, что
-
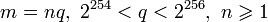 ,
,
где  - порядок группы точек эллиптической кривой
- порядок группы точек эллиптической кривой  , а
, а 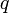 - делитель этого порядка.
- делитель этого порядка.
- Выбрать точку в циклической подгруппе порядка
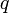 - точку
- точку  .
.
-
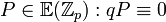 .
.
- Случайно выбирать число
 и вычислить точку
и вычислить точку
-
 ,
,
- Сформировать секретный ключ:

- Сформировать открытый ключ:

Процесс подписи сообщения
- Вычисляет число
 .
.
- Случайно выбирает число
 и вычисляет точку
и вычисляет точку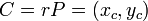 ,
,
если такая точка не существует, то выбирает другое число .
.
- Вычисляет число
 .
.
- Вычисляет число
 .
.
- Формирует подпись
-
 .
.
Процесс проверки подписи
- Проверить условия
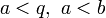 .
.
Если эти условия не выполняются, то подпись отвергается. Если условия выполняются, то процедура продолжается. - Вычислить число
-
 .
.
- Вычислить числа
-
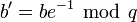 ,
,
-
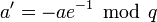 .
.
- Вычислить точку
-
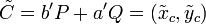 .
.
Если подпись верна, должна получиться исходная точка  .
.
- Проверяет условие
 . Если условие выполняется, то подпись принимается, в противном случае - отвергается.
. Если условие выполняется, то подпись принимается, в противном случае - отвергается.
стр 110
