Сказать "Спасибо"

Полем называется множество 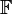 , для которого
, для которого
- заданы операции умножения "
 " и сложения "
" и сложения " ";
";
- выполняются аксиомы группы по сложению "
 " для всего множества
" для всего множества 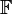 :
:
-
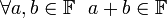
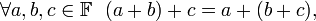
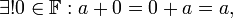
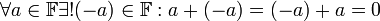 ;
;
- выполняются аксиомы группы по умножению "
 " для множества
" для множества 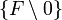
-
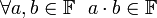
-
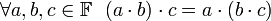
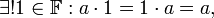
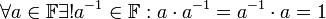 ;
;
- операции сложения и умножения коммутативны
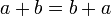 ,
,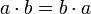 ;
;- выполняется свойство дистрибутивности
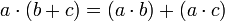 .
.