Система Orphus

Матричные представления в квантовой механике

В случае когда спектр оператора является дискретным, возникают матричные представления. Пусть

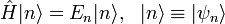
\hat{H}|n\rangle=E_n|n\rangle,~~|n\rangle\equiv|\psi_n\rangle

где n=0,1,2\ldots - индекс состояний дискретного спектра. Из условия полноты

\sum_{n}|n\rangle\langle n|=1

следует, что произвольный вектор состояния |\psi\rangle следующим образом

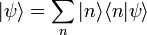|\psi\rangle=\sum_{n}|n\rangle\langle n|\psi\rangle.

Волновая функция 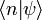\langle n|\psi\rangle в данном n - представлении является матрицами

\langle n|\psi\rangle=\begin{Vmatrix} \langle 1|\psi\rangle\\ \langle 2|\psi\rangle\\ \ldots \end{Vmatrix}

Операторы в n - представлении являются матрицами

\langle n|\hat{A}|\psi\rangle=\sum_{n'}\langle n|\hat{A}|n'\rangle\langle n'|\psi\rangle=
\sum_{n'}A_{nn'}\langle n'|\psi\rangle=\begin{Vmatrix} A_{11}&A_{12}&\ldots\\ A_{21}&A_{22}&\ldots\\ \ldots&\ldots&\ldots \end{Vmatrix}\begin{Vmatrix} \langle 1|\psi\rangle\\ \langle 2|\psi\rangle\\ \ldots \end{Vmatrix}

Барабанов 1 стр 56


Система Orphus

Комментарии