Сказать "Спасибо"

Линейный эффект Штарка в атоме водорода
Линейный эффект Штарка - эффект, при котором уровни атома водорода в однородном электрическом поле испытывают расщепление пропорциональное первой степени напряженности поля. Это связано с наличием у водородных термов случайного вырождения, в силу которого состояния с различными значениями орбитального квантового числа 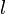 (при заданном главном квантовом числе
(при заданном главном квантовом числе 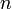 ) обладают одинаковыми энергиями. Матричные элементы дипольного момента для переходов между этими состояниями отнюдь не равны нулю, а потому секулярное уравнение дает уже в первом приближении отличное от нуля смещение уровней.
) обладают одинаковыми энергиями. Матричные элементы дипольного момента для переходов между этими состояниями отнюдь не равны нулю, а потому секулярное уравнение дает уже в первом приближении отличное от нуля смещение уровней.
Для вычисления удобно выбрать невозмущенные волновые функции таким образом, чтобы матрица возмущения была диагональна по отношению к каждой группе взаимно вырожденных состояний. Оказывается, что это осуществляется путем квантования атома водорода в параболических координатах. Волновые функции  стационарных состояний атома водорода в параболических координатах определяются формулами:
стационарных состояний атома водорода в параболических координатах определяются формулами:
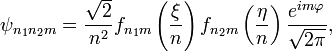

Оператор возмущения (энергия электрона в поле 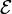 ) есть
) есть 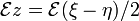 (поле направлено в положительном, а действующая на электрон сила - в отрицательном направлении оси
(поле направлено в положительном, а действующая на электрон сила - в отрицательном направлении оси 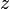 ). Нас интересуют матричные элементы для переходов
). Нас интересуют матричные элементы для переходов  , при которых энергия (т.е. главное квантовое число
, при которых энергия (т.е. главное квантовое число 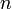 ) не меняется. Легко видеть, что из них оказываются отличными от нуля только диагональные матричные элементы
) не меняется. Легко видеть, что из них оказываются отличными от нуля только диагональные матричные элементы


(мы произвели подстановку  ). В отношении числа
). В отношении числа 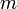 диагональность рассматриваемой матрицы очевидна; что касается чисел
диагональность рассматриваемой матрицы очевидна; что касается чисел 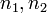 , то диагональность по отношению к ним следует из взаимной ортогональности функции
, то диагональность по отношению к ним следует из взаимной ортогональности функции  с различными
с различными  и одинаковыми
и одинаковыми 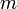 . Интегрирование по
. Интегрирование по  и по
и по  разделяются; получающееся интегралы вычисляются. После простого вычисления получим в результате для поправки первого приближения к уровням энергии
разделяются; получающееся интегралы вычисляются. После простого вычисления получим в результате для поправки первого приближения к уровням энергии
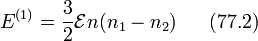
или в обычных единицах
 .
.Две крайние компоненты расщепившегося уровня соответствуют 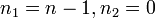 и
и  . Расстояние между этими двумя крайними уровнями есть, согласно
. Расстояние между этими двумя крайними уровнями есть, согласно 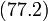 ,
,
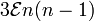 ,
,т.е. общее расщепление уровня при эффекте Штарка примерно пропорционально 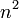 .
.
Ландавшиц 352
