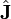$\hat{\bold{J}}$ - оператор углового момента. Безразмерный оператор углового момента вводится формулой:

$\hat{\bold{j}}=\frac{\hat{\bold{J}}}{\hbar}$ .

Оператор квадрата углового момента связан с операторами проекций на координатные оси следующим образом:

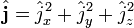$\hat{\bold{j}}=\hat{j}^2_x+\hat{j}^2_y+\hat{j}^2_z$ .

Операторы проекций на координатные оси связаны между собой коммутационными соотношениями:

$[\hat{j}_i,\hat{j}_j]=i\varepsilon_{ijk}\hat{j}_k$ .

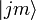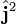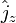Пусть $|jm\rangle$ - это собственные векторы операторов $\hat{\bold{j}}^2$ и $\hat{j}_z$ :

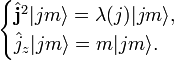
$\begin{cases} \hat{\bold{j}}^2|jm\rangle=\lambda(j)|jm\rangle,\\ \hat{j}_z|jm\rangle=m|jm\rangle. \end{cases}$

Эти собственные векторы ортонормированы:

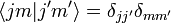
$\langle jm|j'm' \rangle=\delta_{jj'}\delta_{mm'}$

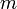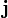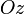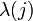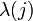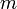По физическому смыслу $m$ - это проекция вектора $\bold{j}$ на ось $Oz$ , $\lambda(j)$ - квадрат длины углового момента. Попробуем разобраться, какие значения могут принимать $\lambda(j)$ и $m$ , пользуясь только коммутационными соотношениями. Разобьем исследование на пункты.

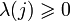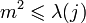1) Покажем, что $\lambda(j)\geqslant 0$ и $m^2\leqslant \lambda(j)$ . Имеем:

$\lambda(j)=\langle jm|\hat{\bold{j}}^2|jm\rangle=\sum_{\alpha=1}^{3}\langle jm|\hat{j}_{\alpha}^2|jm\rangle=\sum^{3}_{\alpha=1}\langle \hat{j}_{\alpha}jm|\hat{j}_{\alpha}jm\rangle\geqslant 0$ ,

Аналогично

$\lambda(j)-m^2=\langle jm|\hat{\bold{j}}^2-j_z^2|jm\rangle=\sum_{\alpha=1}^{2}\langle jm|\hat{j}_{\alpha}^2|jm\rangle=\sum^{2}_{\alpha=1}\langle \hat{j}_{\alpha}jm|\hat{j}_{\alpha}jm\rangle\geqslant 0$ ,

2) Введем операторы

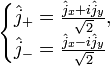
$\begin{cases} \hat{j}_{+}=\frac{\hat{j}_{x}+i\hat{j}_{y}}{\sqrt{2}},\\ \hat{j}_{-}=\frac{\hat{j}_{x}-i\hat{j}_{y}}{\sqrt{2}} \end{cases}$

Тогда

$\begin{cases} \hat{j}_{x}=\frac{\hat{j}_{+}+\hat{j}_{-}}{\sqrt{2}},\\ \hat{j}_{y}=\frac{\hat{j}_{+}-\hat{j}_{-}}{i\sqrt{2}}. \end{cases}$

Также $[\hat{j}_{+},\hat{j}_{-}]=\hat{j}_z$ .

3) Вычислим коммутаторы $[\hat{j}_z, \hat{j}_+]$ и $[\hat{j}_z, \hat{j}_-]$

$[\hat{j}_z, \hat{j}_{\pm}]=\pm\hat{j}_{\pm}.$

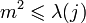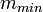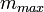a) Если $m^2\leqslant \lambda(j)$ , то существуют $m_{min}$ и $m_{max}$ . Очевидно, что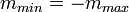 $m_{min}=-m_{max}$

б) 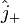$\hat{j}_{+}$ и $\hat{j}_{-}$ - операторы повышения и понижения.

4) Воспользовавшись оператором понижения $\hat{j}_{-}$ , запишем:

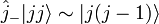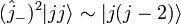$\hat{j}_{-}|jj\rangle\sim|j(j-1)\rangle$ , $(\hat{j}_{-})^2|jj\rangle\sim|j(j-2)\rangle$ , $\ldots$ $(\hat{j}_{-})^N|jj\rangle\sim|j(j-N)\rangle,~~~~N\in\mathbb{Z}.$

Предположим, что таким образом мы осуществляем переход от состояния с максимальной проекцией 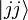$|jj\rangle$ к состоянию с минимальной проекцией 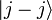$|j-j\rangle$ . Тогда

$j-N=-j,$

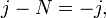
то есть

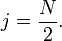
$j=\frac{N}{2}.$

Следовательно 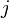$j$ может принимать либо целые, либо полуцелые значения.

5) Найдем 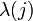$\lambda(j)$

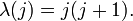
$\lambda(j)=j(j+1).$

Барабанов 1 81

Сказать "Спасибо"

Система собственных векторов операторов

Комментарии