Общее решение уравнения Шредингера

$\psi(\bold{r})=\psi_{0}(\bold{r})+\psi_{1}(\bold{r})$ ,

принимает вид:

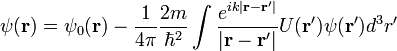$\psi(\bold{r})=\psi_{0}(\bold{r})-\frac{1}{4\pi}\frac{2m}{\hbar^2}\int\frac{e^{ik|\bold{r}-\bold{r}'|}}{|\bold{r}-\bold{r}'|}U(\bold{r}')\psi(\bold{r}')d^3 r'$ .

Это решение является, конечно, формальным. В самом деле под интегралом в правой части стоит та же неизвестная функция 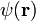$\psi(\bold{r})$ , что и в левой части. Поэтому правильнее было бы сказать, что мы выполнили переход от дифференциального уравнения Шредингера к эквивалентному интегральному уравнению.

Заметим, что подынтегральное выражение в правой части отлично от нуля только в области, где $r'<a$ . Следовательно

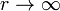$r'<a\ll r$ при $r\to\infty$ ,

т.е. при переходе к асимптотике 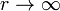$r\to\infty$ возникает малый параметр $r'/r$ . Разложение по этому малому параметру дает:

$|\bold{r}-\bold{r}'|\simeq r-\bold{r}'\bold{n},~~~\bold{n}=\frac{\bold{r}}{r},$

$\frac{e^{ik|\bold{r}-\bold{r}'|}}{|\bold{r}-\bold{r}'|}\simeq \frac{e^{ikr-ik\bold{r}'\bold{n}}}{r}$ .

Мы пренебрегаем всеми слагаемыми в волновой функции, которые с ростом $r$ падают быстрее, чем $1/r$ .

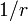Итак, волновая функция 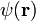$\psi(\bold{r})$ в асимптотике принимает вид:

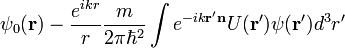$\psi(\bold{r})|_{r\to\infty}=\psi_0(\bold{r})-\frac{m}{2\pi\hbar^2}\int\frac{e^{ikr}e^{-ik\bold{r}'\bold{n}}}{r}U(\bold{r}')\psi(\bold{r}')d^3 r'=$ $\psi_0(\bold{r})-\frac{e^{ikr}}{r}\frac{m}{2\pi\hbar^2}\int e^{-ik\bold{r}'\bold{n}}U(\bold{r}')\psi(\bold{r}')d^3 r'$ .

Ранее мы предположили, что волновая функция в асимптотике должна иметь следующую форму:

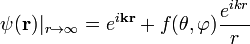$\psi(\bold{r})|_{r\to\infty}=e^{i\bold{kr}}+f(\theta,\varphi)\frac{e^{ikr}}{r}$ .

Легко видеть, что, взяв в качестве решения $\psi_0$ однородного уравнения плоскую волну,

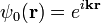$\psi_0(\bold{r})=e^{i\bold{kr}}$ ,

мы получаем точно то, что и ожидали. При этом амплитуда рассеяния определяется следующей формулой:

$f(\theta,\varphi)=-\frac{m}{2\pi\hbar^2}\int e^{-ik\bold{n}\bold{r}'}U(\bold{r}')\psi(\bold{r}')d^3r'$ .

Таким образом, мы осуществили переход от исходного дифференциального уравнения Шредингера к интегральному уравнению следующего вида:

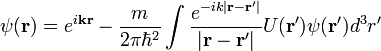
$\psi(\bold{r})=e^{i\bold{kr}}-\frac{m}{2\pi\hbar^2}\int \frac{e^{-ik|\bold{r}-\bold{r}'|}}{|\bold{r}-\bold{r}'|}U(\bold{r}')\psi(\bold{r}')d^3 r'$

В асимптотике 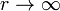$r\to\infty$ решение этого уравнения имеет требуемый вид. Само уравнение называют интегральным уравнением теории рассеяния.

Барабанов 2 стр 87

Сказать "Спасибо"

Интегральное уравнение для задачи рассеяния

Комментарии