Сказать "Спасибо"
Принцип минимальности термодинамических потенциалов
В состоянии теплового равновесия свободная энергия  и термодинамический потенциал
и термодинамический потенциал  тела минимальны - первая по отношению ко всем изменениям состояния при постоянных
тела минимальны - первая по отношению ко всем изменениям состояния при постоянных 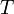 и
и  , а второй - по отношению к изменениям состояния при постоянных
, а второй - по отношению к изменениям состояния при постоянных 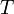 и
и  .
.
Доказательство справедливости принципа
Рассмотрим необратимый процесс установления термодинамического равновесия в замкнутой системе, состоящей из малой подсистемы - тела 1 и термостата 2. Пусть в начальный момент времени тело находится в состоянии частичного внутреннего равновесия, таком, что некоторый параметр тела, например, магнитный момент  отличен от своего термодинамически равновесного значения
отличен от своего термодинамически равновесного значения  . Будем считать, что в ходе процесса релаксации у тела может меняться не только
. Будем считать, что в ходе процесса релаксации у тела может меняться не только  , но и
, но и 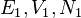 при условии сохранения полных энергии, объема и числа частиц
при условии сохранения полных энергии, объема и числа частиц  и
и 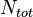 .
Необратимые процессы сопровождаются уменьшением одного из термодинамических потенциалов. Производная по времени от суммарной энтропии такой системы
.
Необратимые процессы сопровождаются уменьшением одного из термодинамических потенциалов. Производная по времени от суммарной энтропии такой системы
равна
В течение необратимого процесса температура, давление и химический потенциал термостата практически не меняются и фактически играют роль внешних условий для малой подсистемы. В дальнейшем параметры термостата будем писать без индекса 2.
Поскольку при необратимом процессе полная энтропия замкнутой системы может только расти 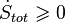 , то из
, то из  получаем неравенство:
получаем неравенство:
Необратимые процессы сопровождаются уменьшением одного из термодинамических потенциалов.